Spring semester 2010 I ran a mathematical modeling course on protein-protein interaction networks in cells.

Interactions between proteins in cells are critical to the functioning of a cell.

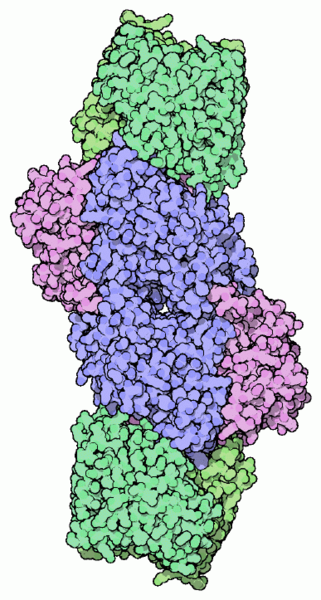
The bacterial nitrogenase enzyme is formed by a protein-protein interaction between two copies of two different proteins. One protein is shown in shades of green, the other in shades of blue and purple.

The collection of all proteins in a cell forms a network with the proteins as the points, or vertices, of the network, and interactions between proteins indicated by lines, or edges:

Network visualisation of the human cellular interaction network, where each point represents a protein and each blue line between them is an interaction.

In these networks an important role is played by cliques. These are collections of proteins in which each protein in the collection interacts with every other protein in the collection. In graph-theoretic terms, they are complete subgraphs. Finding cliques in protein-protein networks is a problem of biological significance (a, b, c)

The problem of finding cliques (=complete subgraphs) in a network -the clique problem – is NP complete, so if then there is no fast algorithm to solve this problem.

Leanne Silvia began as an honors student in our undergraduate computational science program when she was a freshman. Spring 2010 she was a student in the mathematical modeling course referred to above, and she became interested in the clique-problem, to the extent that she worked on it as a research project Summer 2010, as a student in our computational science program [lsilvia_siam2010poster].

Mathematica has in-built algorithms (in Combinatorica) to find maximal cliques. Leanne’s algorithm finds all cliques, and over a certain size of graph, does it faster than existing Mathematica algorithms. This Fall, as a beginning junior she will be presenting her research at the Wolfram Technology Conference in Champagne, IL. Her algorithm may prove to be especially useful to biologists working in this area.

x

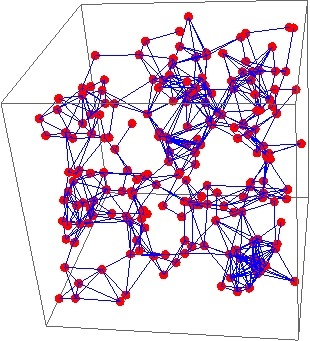
Leanne is working now on applying her algorithm for finding cliques to random geometric graphs. These are graphs formed by placing a number of points – in a plane or in space – randomly, and joining points by an edge if they are “close” – i.e. within a specified distance of each other.

Random geometric graphs have, over the last few years, come to be regarded as a good model for protein-protein interaction networks. Therefore, any algorithm that finds all cliques in random geometric graphs – at least for a range of total number of points – will be of interest to biologists working on protein-protein interactions.

A random geometric graph in a unit cube: 200 uniformly random points, which are joined pairwise if they are less than 0.2 apart