In an earlier post, I wrote that my colleague Sigal Gottlieb was annoyed by her own approach at automatically solving the following problem – which she had asked of her elder son – via algebra, rather than thinking through the problem in a more direct way:

In a large group of children there are 3 boys for every 2 girls. 30 boys leave the group and then in the smaller group that’s left there are 2 boys for every 3 girls. How many boys and girls were there in the original group?

To give the same flavor of the problem but make it a little easier for her younger son, she asked him:

Two children Amy and Bob, each have collections of books. Bob has twice as many books as does Amy. Amy’s mother buys her 24 new books and then Amy has twice as many books as does Bob. How many books did Amy and Bob have to begin?

The second problem

Let’s look at the second problem diagramatically:

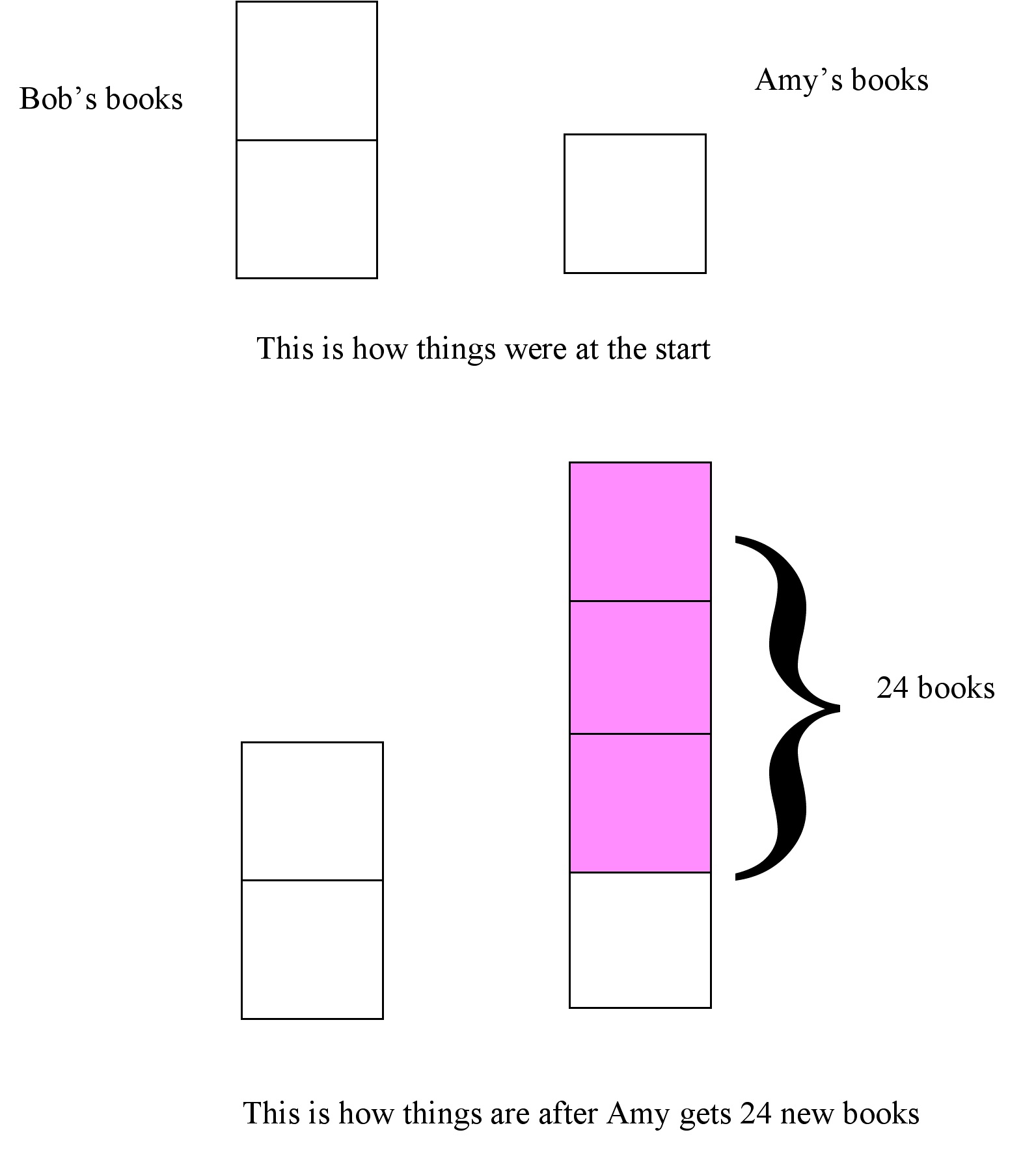In this diagram we imagine Bob and Amy’s books to be evenly distributed in boxes: each box holds the same number of books.

Bob has two boxes of books to Amy’s one box.

Amy then gets 24 more books.

Bob’s books stay the same so Amy has some more boxes.

In order to have a ratio of 2 to 1 Amy gets 3 extra boxes.

So 3 boxes, each with the same number of books, holds 24 books. Therefore 1 box holds 8 books.

So originally Bob, with 2 boxes, had 16 books and Amy, with 1 box, had 8 books.

The first problem

The first problem can be approached diagramatically in much the same way, but a little adjustment is in order because of the slightly more awkward ratio of 3:2

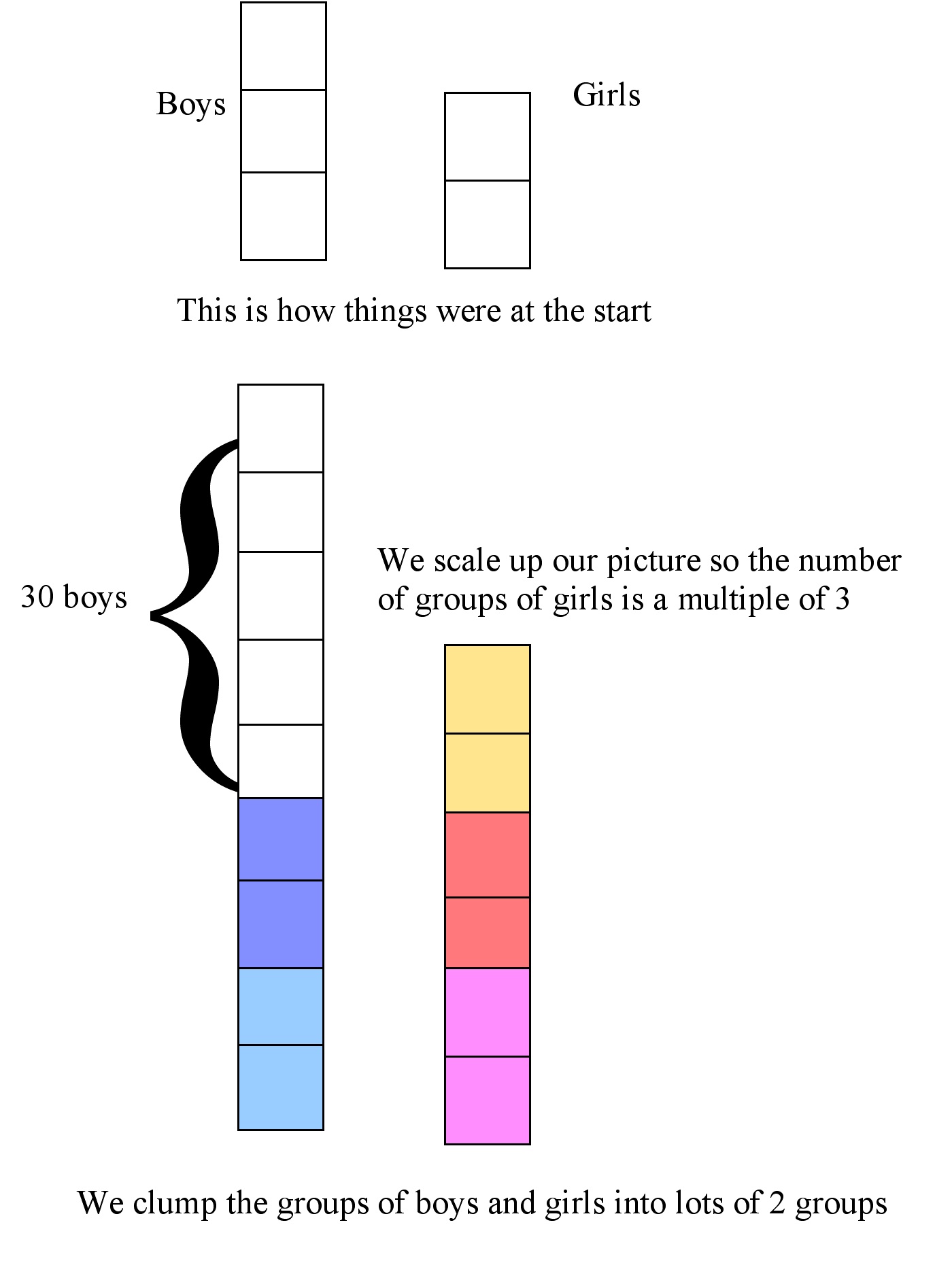In this diagram we begin with 5 equal size groups : 3 groups of boys and 2 groups of  girls.

We want to end up with a ratio the other way around, so one sensible thing to do is to scale up the picture by scaling the numbers of boys and girls by a factor of 3.

Then there are 9 groups of boys and 6 groups of girls – still a ratio of 3:2 for boys to girls.

Now let’s clump the groups into lots of 2, as shown by the coloring.

The girls now consist of 3 lots, each lot being 2 groups.

So the boys, after 30 leave, will have to be 2 lots, again each lot being 2 groups: 4 groups in all.

So, 9-4=5 groups of boys departed, and these 5 equal groups totaled 30 boys.

Therefore, 1 group has 6 students.

So originally there were 54 boys (9 groups of 6) and 36 girls (6 groups of 6).

Algebra

Of course algebra is pretty sweet too, just being arithmetic on names.

So, in the first problem, let b be the number of boys at the start, and g the number of girls.

Because there are 3 boys for every 2 girls we know that 2b=3g (think about it for a minute: it’s not the other way around, because “b” doesn’t stand for “boys” – it stands for “number of boys”, and “g” stands for “number of girls”, not “girls”).

After b has decreased by 30 we have b-30 boys and a ratio of 3 girls for every 2 boys.

So, 2g=3(b-30) (again think about it for a minute: it’s still not the other way around).

Let’s do some arithmetic on these names:

2g=3b-90 so 6g=9b-270.

Also, from 2b=3g we see that 4b=6g.

Combining these we see that 9b-270=4b.

Therefore, 5b=270 so b=54.

Then 3g=2b=108 so g=36. Ta-dah!

Notice I carefully avoided using fractional quantities.

Does it feel to you, as it does to me, that the diagrammatic solution and the algebraic solution seem to utilize different parts of our brains?