Central ideas of school mathematics: Patterning
Posted by: Gary Ernest Davis on: September 17, 2010
My colleague Robert Hunting – now back in Australia after several years in East Carolina – has got me interested in a project on “big ideas” in school mathematics. I want to discuss some of our thinking on this project in posts on this blog. Rather than refer to “big ideas” I will take the liberty of using the term “central ideas”. These are ideas that I see as central to school mathematics if that subject is to avoid total disconnection with the rapidly changing world of professional and applied mathematics.
The most basic ball-park characterization of mathematics is that it is a human activity concerned with scientific study of number, space, and arrangement, and applications of this science to other areas of human activity.
A basic principle of school mathematics that follows from this is that mathematics is not just about formulas, memorized facts, and clever ways of calculating, but it is about central scientific issues in the areas with which mathematics deals. This is similar in principle to the teaching of other sciences – physics, chemistry and biology are not the same subjects in school now that they were in 1930. Yet current school mathematics by and large IS the same subject as was taught in school in 1930, with the exception of the use of technology – largely calculators – to carry out calculations.
So in discussing central ideas of school mathematics it seems imperative to reflect on where the science of mathematics is now headed, what are its pressing concerns, and what new findings are relevant to school mathematics. For if we do not focus on these issues then school mathematics runs the very severe risk of becoming irrelevant to the fast-changing practice of the science of mathematics and its applications.
Patterns
In the scientific field that is mathematics one feature that stands out very strongly is that of patterns. Patterns are the basic building blocks on which mathematics is formed. There is a mathematical and psychological progression in dealing with patterns:
Recognition
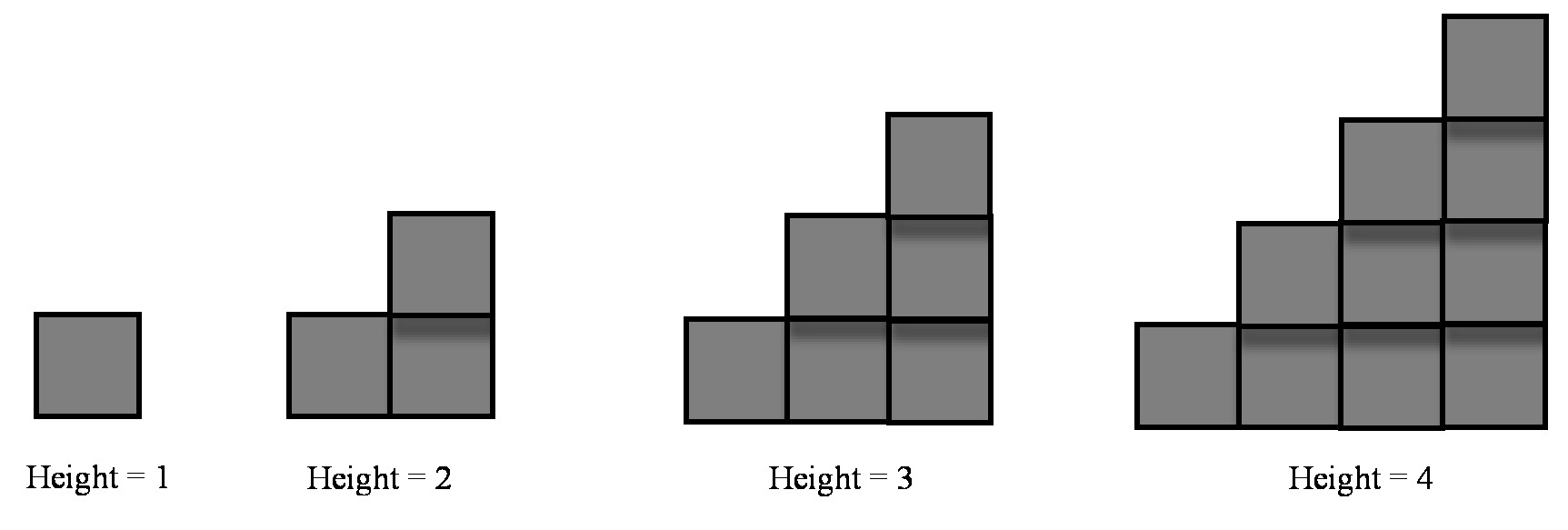
The first and most basic step in patterning is the dawning recognition that there is a pattern to be observed. Often learners can feel in their bones that there is a pattern but cannot, yet, find the words to describe that pattern. This is a common experience for all teachers of mathematics. Here is an example. Students are building staircases out of boxes as follows:
A student may begin to feel there is a pattern to the number of boxes needed to build a staircase, but not be able to articulate that pattern.
This may be the case even if they have constructed a table:
|
Heightof staircase |
Total number of boxes |
| 1 | 1 |
| 2 | 3 |
| 3 | 6 |
| 4 | 10 |
In a table like this a student might see the numbers are going up by 1, then 2, then 3, then 4, but not be able to articulate this clearly.
Articulation
The next logical, and psychological, step in patterning is the ability to articulate a pattern. This is done declaratively through speech, through writing, through the use of diagrams, or through bodily movements such as waving and gesturing. All these activities are indications of an ability to articulate a pattern. The written form has, for millennia, been privileged over other forms of articulation, but with the widespread use of recording media there is no cogent reason why that should be so nowadays.
In the staircase example above a student may be able to articulate that the number of boxes is increasing each time and the amount of increase is also increasing, by 1 each time.
Another observation that student might make and articulate is that the staircases are a little over half a square:
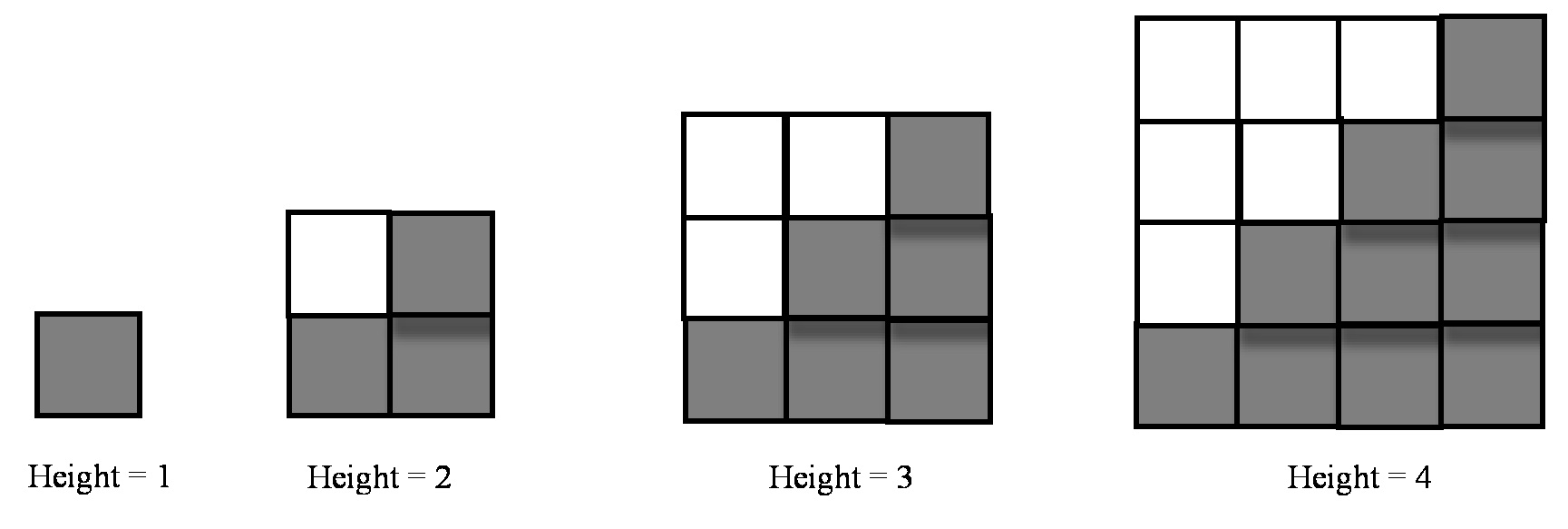 The white pieces match the gray boxes below the diagonal to complete a square.
The white pieces match the gray boxes below the diagonal to complete a square.
Generality
This step is difficult even for many teachers of mathematics especially, in my experience, elementary teachers. It is how to express the general pattern using variables. These variables do not have to be standard mathematical symbols such as “xâ€, “yâ€, “m†or “nâ€. The variables can be words of the common language.
In the staircase example an expression of what happens in the general case, rather than a few particular cases, might be something like this:
“The number of boxes needed for a given height is the number of boxes needed for height 1 less, plus the height.”
Another, fancier, way of saying this, is where
is the height of a staircase and
is the number of boxes needed to build a staircase of height
.
The developmental and psychological point is not simply the expression of the pattern in more or less standard mathematical symbols as compared with natural language variables. Rather, it is the empirically observed difficulty that many students, and teachers, have in moving from specific numbers – such as 1, 2, 3 , 4 – to a general case. This is the focus of mathematical education as a discipline, as compared with mathematics per se. The focus of attention on the general case is necessary for further development in mathematical fluency, relating to algebra and functions (to take two examples).
In terms of adding extra boxes to the staircase to complete a square, an expression of what happens in the general case, rather than a specific value for he height of the staircase, might go something like this:
“The number of boxes needed is the height of the staircase, which is the same as the length of the diagonal, plus half the square of the height.”
Explanation
Following on the ability to express a process in generality, rather than simply through a short list of specific instances, is an indispensable and essential ingredient of mathematics: explanation of why the articulated general pattern holds good.
Explanation not only explains that the observed general case holds good, but usually gives insights into why.
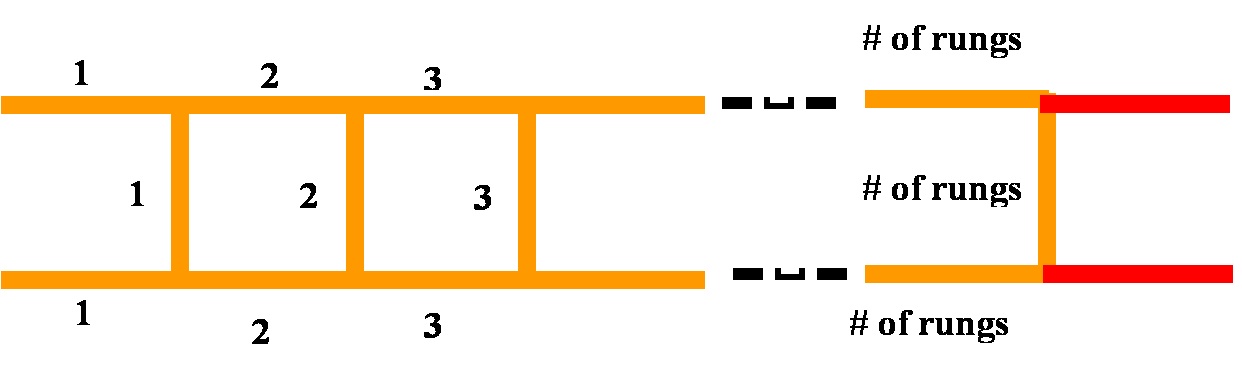
Consider the following very simple construction of building a series of ladders:
 Typically in elementary or middle school students are taught to make table, as a preliminary to recognizing and articulating a pattern:
Typically in elementary or middle school students are taught to make table, as a preliminary to recognizing and articulating a pattern:
| Number of rungs | Number of pieces of wood needed to build the ladder |
| 1 | 5 |
| 2 | 8 |
| 3 | 11 |
| 4 | 14 |
|
5 |
17 |
An articulation of a recognized pattern (“it’s going up by 3″) might be something like: ‘”the number of pieces of wood starts with 5 and then increases by 3 every time a new rung is added.”
This is usually where elementary and middle school teachers stop, regarding the exercise as particularly successful if students can get this far in patterning: “spot the pattern, say the pattern.”
Expression of the general case using variables, which is less common in elementary and middle school mathematics, might go something like this:
“The number of pieces of wood needed is 3 times the number of rungs plus 2.”
This articulated general case comes from a numerical table. It does not, yet, reflect the process used in constructing the ladders, which is what will tell us why this general case holds good. Focusing on the process of building the ladders gives us an explanation:
Each rung can be group with 2 other pieces of wood and that leaves 2 pieces of wood over at the end.
______________________________________________________________________________
Patterning is, in my view, a central idea in school mathematics simply because it is central in all mathematical activity, and can be approached through relatively simple examples, many from applications.
Patterning in its fuller version from recognition, through articulation, and generality to explanation is not well addressed in elementary and middle school. It needs to be so addressed if students are to build strong mathematical foundations that prepare them for overall mathematical fluency.

September 17, 2010 at 8:48 am
Love the focus on Central Ideas! Our district in Ontario is focused on Big Ideas. I like the distinction of “Central” rather than “Big”. We’re talking about the location rather than the size of the idea! That’s funny.
Math for me is all about ideas, the excitement of exploration, the achievement of organized thought, the abstract and the infinite, the conception of a greater reality! Those may not be the Central Ideas in learning math, though, they are some Big Ideas that inspire me.
Dr. Marion Small is a leader here, having published “Big Ideas from Dr. Small”, she connected to NCTM, http://www.nelson.com/ned/#cmd%2Fauthor%3Fid%3D120182 The books are scholarly yet down-to-earth, practical.