Why, when we round n+sqrt(n), do we never get a square?
Posted by: Gary Ernest Davis on: November 28, 2010
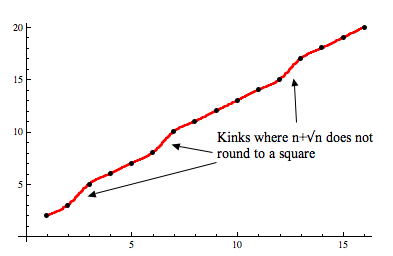
Jim Tanton (@jamestanton) Tweeted recently that for a positive integer , rounded to the nearest integer, is never the square of an integer.
This certainly seems to be borne out by a few calculations (carried out in Excel, using the built-in “round’ function):
| n | n+sqrt(n) | round(n+sqrt(n)) |
| 1 | 2 | 2 |
| 2 | 3.414213562 | 3 |
| 3 | 4.732050808 | 5 |
| 4 | 6 | 6 |
| 5 | 7.236067977 | 7 |
| 6 | 8.449489743 | 8 |
| 7 | 9.645751311 | 10 |
| 8 | 10.82842712 | 11 |
| 9 | 12 | 12 |
| 10 | 13.16227766 | 13 |
| 11 | 14.31662479 | 14 |
| 12 | 15.46410162 | 15 |
| 13 | 16.60555128 | 17 |
| 14 | 17.74165739 | 18 |
| 15 | 18.87298335 | 19 |
| 16 | 20 | 20 |
| 17 | 21.12310563 | 21 |
| 18 | 22.24264069 | 22 |
| 19 | 23.35889894 | 23 |
| 20 | 24.47213595 | 24 |
| 21 | 25.58257569 | 26 |
| 22 | 26.69041576 | 27 |
| 23 | 27.79583152 | 28 |
| 24 | 28.89897949 | 29 |
| 25 | 30 | 30 |
| 26 | 31.09901951 | 31 |
| 27 | 32.19615242 | 32 |
| 28 | 33.29150262 | 33 |
| 29 | 34.38516481 | 34 |
| 30 | 35.47722558 | 35 |
| 31 | 36.56776436 | 37 |
| 32 | 37.65685425 | 38 |
| 33 | 38.74456265 | 39 |
We see that the square numbers 4, 9, 16, 25 and 36 are indeed missing from this table.
Why should this be so?
I am going to use an argument due to David Ratcliffe (@daveinstpaul)Â that splits into two different cases and uses an argument by contradiction, which is part of a series of techniques that mathematicians use that go by the general name of “counterfactuals”.
Terry Tao has written extensively about these sort of arguments, The general idea is that we set up a world that we believe cannot exist – sort of like in science fiction, but math fiction. Then we carefully examine this world for consequences and see if something truly unacceptable occurs. If it does, we conclude that no such world can exist.
The world we set up is one in which, contrary to our empirical observations, there is an instance of a positive integer for which rounding
to the nearest integer gives us a square number, which we will name
.
What does rounding to get
mean, in a way that allows us to think about consequences?
It means that .
How can we use this imaginary scenario to draw conclusions, hopefully very strange ones?
Let’s think about the following two mutually exclusive cases, at least one of which must hold good:
.
In this case imagine, counterfactually, that .
Then .
This contradictory state of affairs means that, in this case, we have .
Then
2. .
In this case, because is an integer, we have
.
In this case, imagine, again counterfactually, that .
Then , contrary to
.
Again, this contradictory state of affairs means that, in this case, we have .
Then .
In either case, does not lie between
as we assumed counterfactually.
This contradictory state of affairs means that, contrary to what we asserted in our counterfactual world, we can never round to obtain the square of an integer.
2 Responses to "Why, when we round n+sqrt(n), do we never get a square?"
[…] Republic of Mathematics Blog has a nice indirect proof of a problem that James Tanton posted on twitter, that when we round n+sqrt(n), for integer n, we […]

November 28, 2010 at 7:54 pm
Nice!
I did some work on this in R on the difference between n + n**.5 and k^2. It follows an interesting pattern, peaking and valleying. The relative minima get arbitrarily close to .5.
CODE STARTS
a <- 100000
n <- 1:a
nrn <- n + n^.5
nsq <- n^2
diff <- vector('numeric', 100)
for (i in 1:a){
diff[i] <- min(abs(nrn[i] – nsq))
}
CODE ENDS
I also made plots
plot(n, diff)
plot(n[diff<.6], diff[diff < .6])
plot(n[position], diff[position])
The first two are better with a smaller range of N.
By n = 100,000 the smallest minimum is pretty close to .5 – it is 0.500396