Geodesic paths and their daughters (on a rectangular grid)
Posted by: Gary Ernest Davis on: November 30, 2010
Walks on a grid
On the rectangular grid shown below we can imagine walking from the red spot to a yellow spot, by taking unit steps up, down, left or right, to adjacent spots:
There are many ways to walk from the red spot to the purple spot shown below, but only 2 of those paths – the ones show in color – are shortest paths:
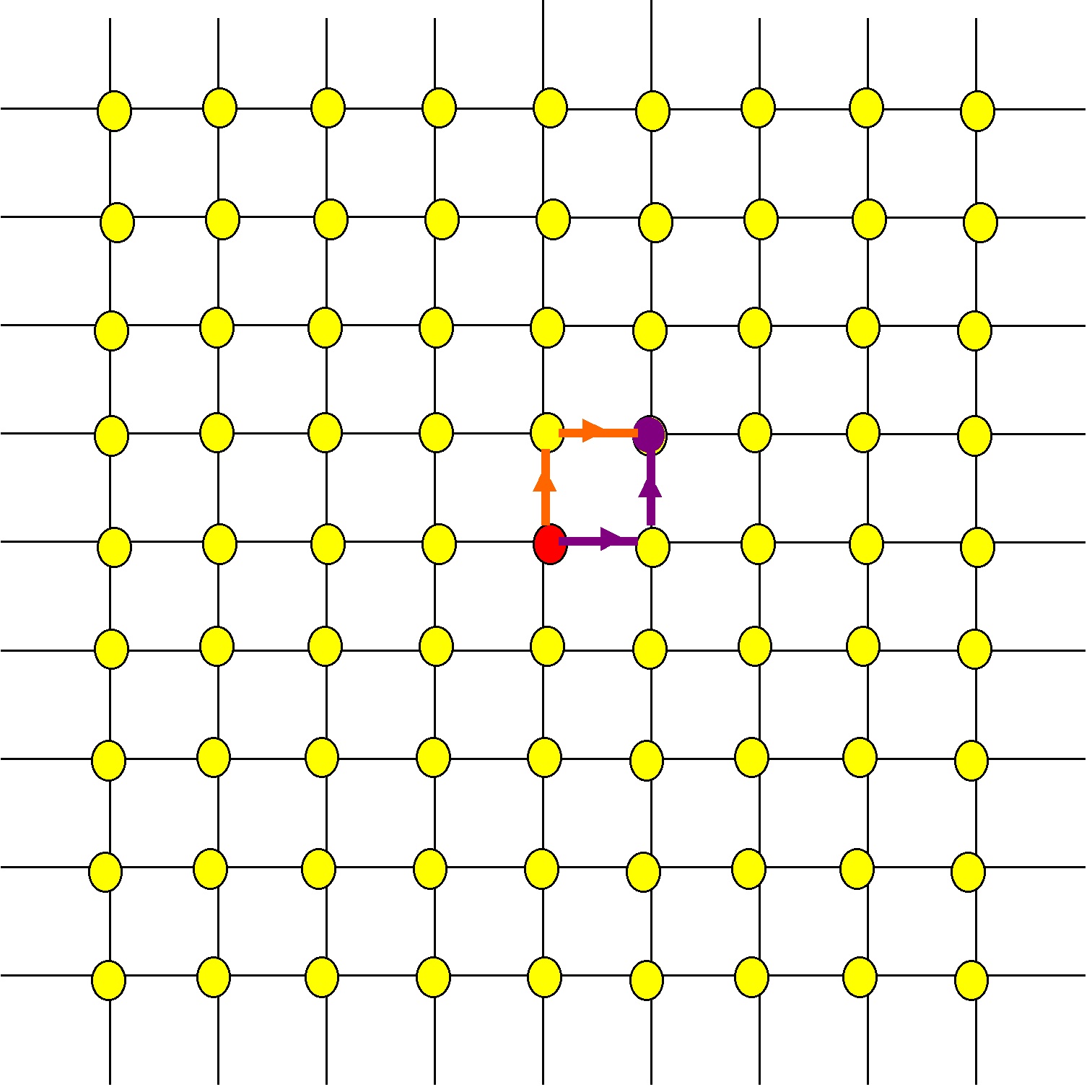 All other paths from the red spot to the purple spot take more than two steps.
All other paths from the red spot to the purple spot take more than two steps.
Geodesic paths and their daughters
We call a shortest path from the red spot to a yellow spot a geodesic.
The length of a geodesic is the number of yellow spots it passes through.
The geodesics shown above in color have length 2.
I want to think about the idea of a geodesic having offspring.
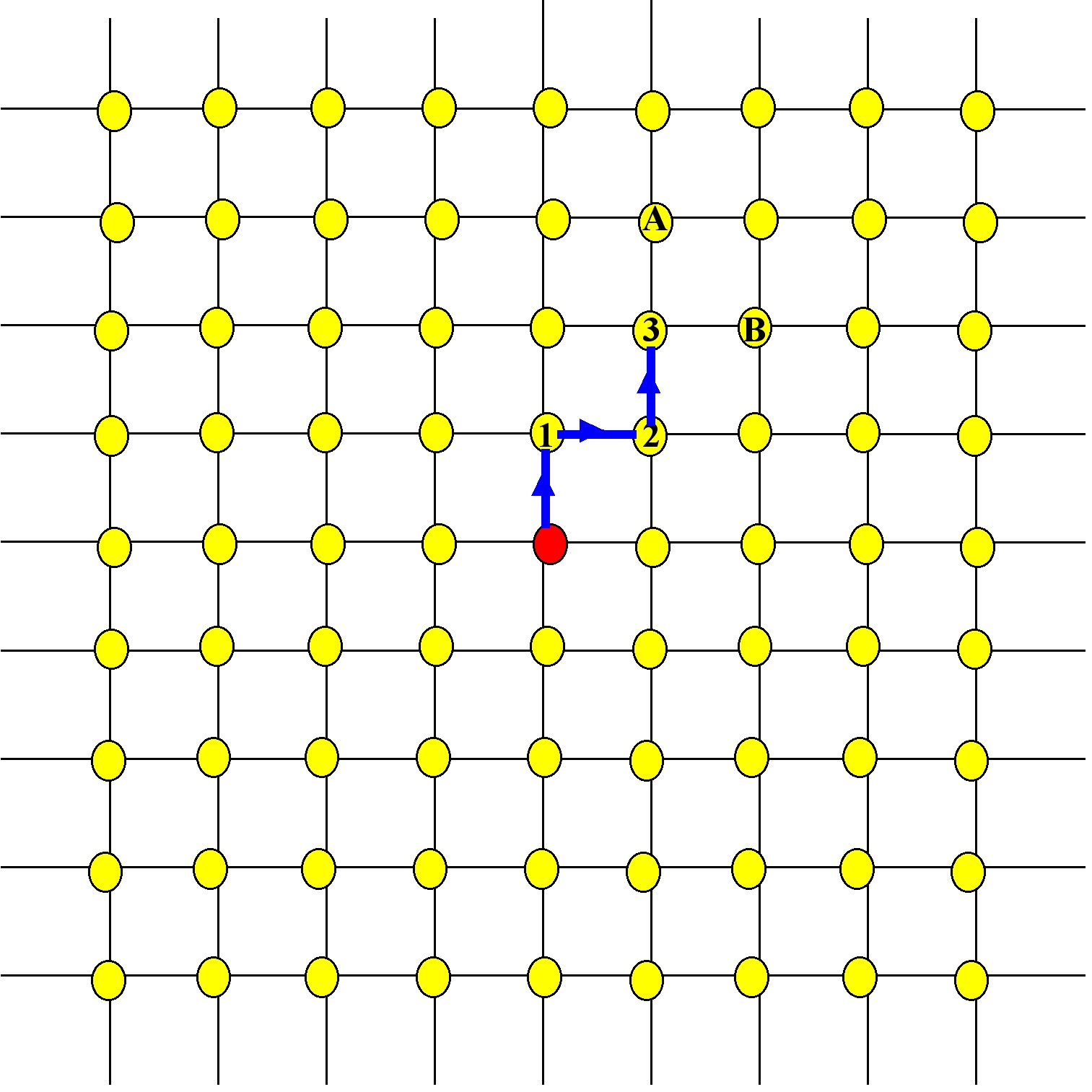
Suppose a geodesic goes from the red dot to yellow dot 1, then to yellow dot 2, and to yellow dot 3:
This geodesic, which we will name (Greek “gamma”) has length 3: it passes through 3 yellow dots.
It is also a part of 2 geodesics of length 4, namely those geodesics that after reaching yellow spot 3, go to yellow spot A, or to yellow spot B.
These length 4 geodesics we call daughters of the geodesic : they are geodesics of length one greater than
and they consist of the path
plus one extra step.
The geodesic has 2 daughters, and this is typical of most geodesics.
However, some geodesics have 3 daughters. These are the geodesics that travel directly up, or directly down, or directly left, or directly right, from the red spot:
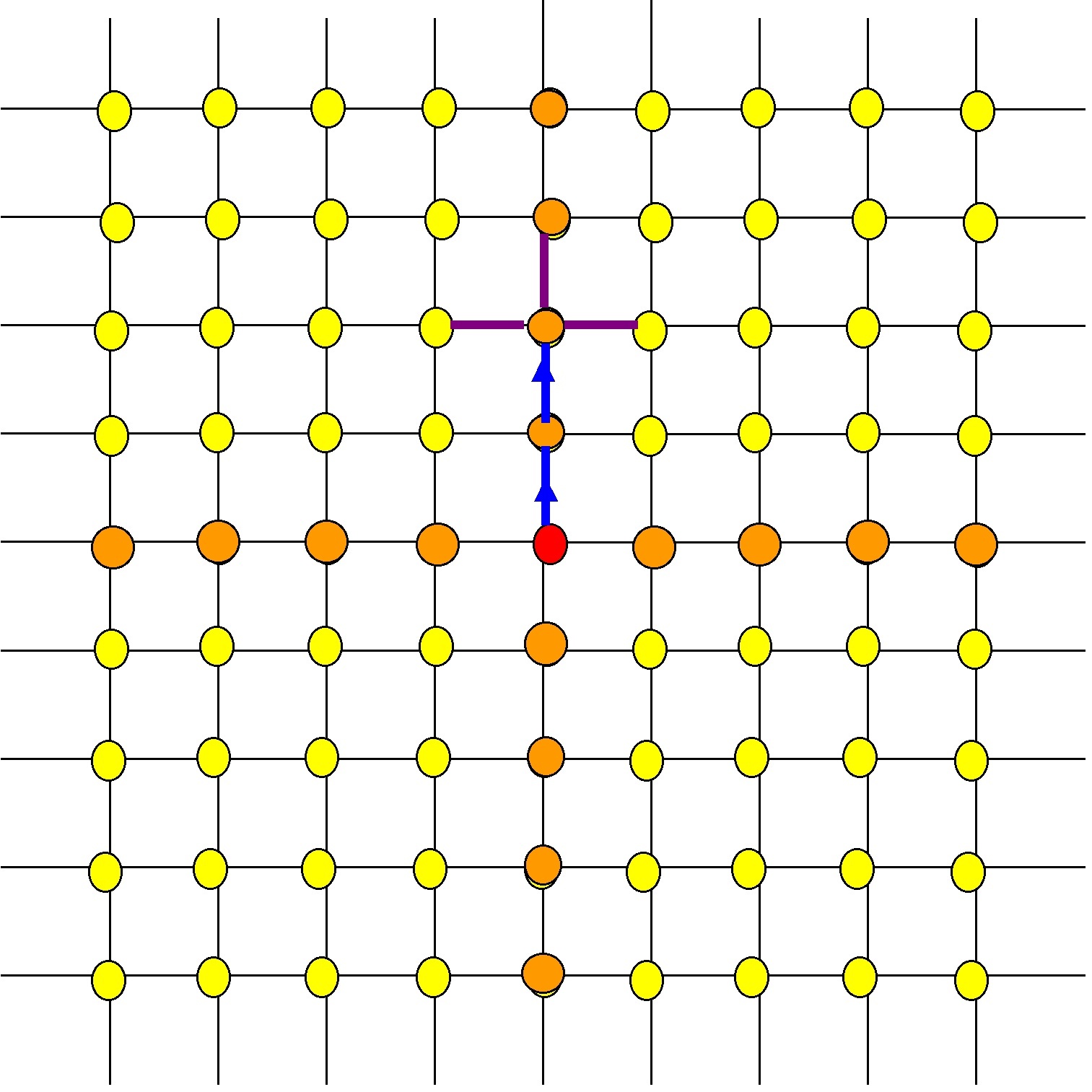 The blue geodesic (of length 2) has 3 daughters (of length 3).
The blue geodesic (of length 2) has 3 daughters (of length 3).
A recurrence for the number of geodesics of a given length
Let’s call a geodesic of type A if it has 2 daughters, and of type B if it has 3 daughters.
Let denote the number of geodesics of type A that have length
, and let
denote the number of geodesics of type B that have length
.
There are 4 geodesics of length 1, all of which are of type B.
So .
A geodesic of type A of length has 2 daughters, both of which are of type A, and of length
.
A geodesic of type B of length has 3 daughters, all of length
, two of which are of type A and the other of which is of type B.
So, .
This means
The recurrence together with the initial condition
allows us to calculate how many geodesics there are of type A of length
, for any
.
The total number of geodesics of length we denote by
, so
.
From the recurrence for and the fact that
we get the same recurrence for
as for
, but with a different initial condition:
.
A spreadsheet can calculate the values of for small
from the recurrence formula:
| n | Gamma(n) | Gamma(n)/Gamma(n-1) |
| 1 | 4 | |
| 2 | 12 | 3 |
| 3 | 28 | 2.333333333 |
| 4 | 60 | 2.142857143 |
| 5 | 124 | 2.066666667 |
| 6 | 252 | 2.032258065 |
| 7 | 508 | 2.015873016 |
| 8 | 1020 | 2.007874016 |
| 9 | 2044 | 2.003921569 |
| 10 | 4092 | 2.001956947 |
| 11 | 8188 | 2.000977517 |
| 12 | 16380 | 2.00048852 |
| 13 | 32764 | 2.0002442 |
| 14 | 65532 | 2.000122085 |
| 15 | 131068 | 2.000061039 |
| 16 | 262140 | 2.000030519 |
| 17 | 524284 | 2.000015259 |
| 18 | 1048572 | 2.000007629 |
| 19 | 2097148 | 2.000003815 |
| 20 | 4194300 | 2.000001907 |
| 21 | 8388604 | 2.000000954 |
| 22 | 16777212 | 2.000000477 |
| 23 | 33554428 | 2.000000238 |
| 24 | 67108860 | 2.000000119 |
| 25 | 134217724 | 2.00000006 |
How the number of geodesics grows as the length increases
Also shown in this table is the ratio .
This ratio seems to approach 2 as increases.
This numerical evidence suggests that the total number of geodesics of length is increasing exponentially, by a multiplication factor of about 2.
To see why approaches a limit as
increases, as distinct from observing from a table that it seems to, we use the fact that
so
.
Because increases without bound, we see that
for large
, as the numerical evidence suggested.
What next?
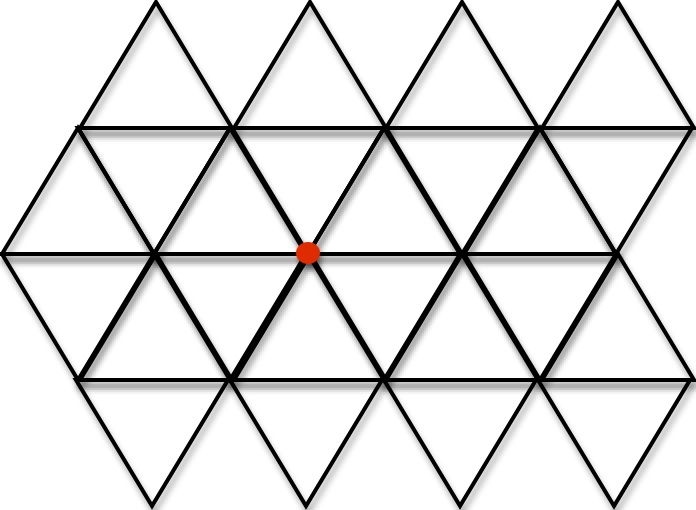
The rectangular grid could be replaced by a triangular grid:
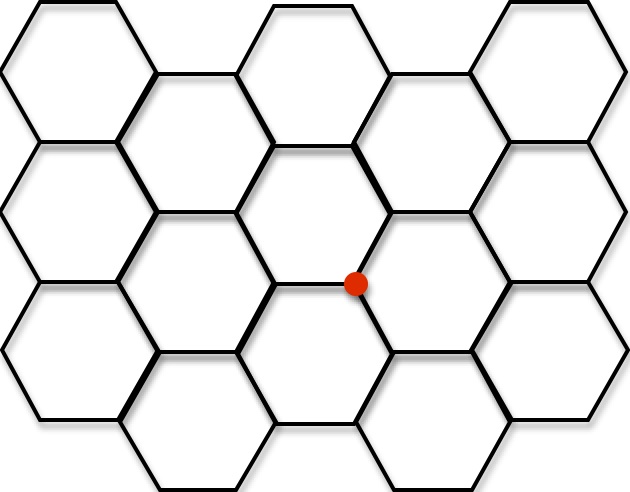
or a hexagonal grid:
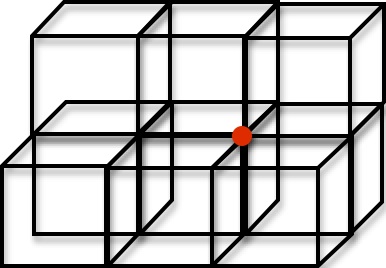
Venturing into 3 dimensions, we could consider a cubical grid:
How does the number of geodesics from a given starting spot vary with the length of the geodesic in each of these cases?

December 1, 2010 at 1:10 am
Square grid: 2^n – 4
Triangular grid: 6*(2^n – 1)
Hexagonal grid: 6*(2^(n/2)-1) if n is even; 9*[2^((n-1)/2)]-6 if n is odd.
Cubical grid: 8*3^n – 12*2^n + 6
The formula for the hexagonal grid can be found here:
http://oeis.org/A061776
The last two sequences are missing from the OEIS. All of the above formulas assume n>0. The formula for the cubical grid can be generalized to higher dimensions.
December 1, 2010 at 6:04 am
Thanks for the information and links, Dave