Why, when we round n+sqrt(n), do we never get a square?

Posted by: Gary Ernest Davis on: November 28, 2010

In: Uncategorized
Comment!

0 Shares

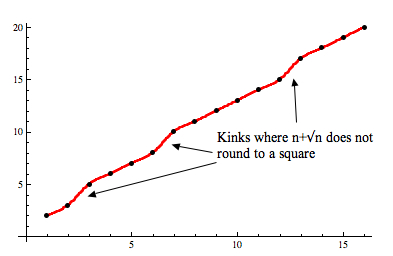
Jim Tanton (@jamestanton) Tweeted recently that for a positive integer $n, n+\sqrt{n}$ , rounded to the nearest integer, is never the square of an integer.

This certainly seems to be borne out by a few calculations (carried out in Excel, using the built-in “round’ function):

n	n+sqrt(n)	round(n+sqrt(n))
1	2	2
2	3.414213562	3
3	4.732050808	5
4	6	6
5	7.236067977	7
6	8.449489743	8
7	9.645751311	10
8	10.82842712	11
9	12	12
10	13.16227766	13
11	14.31662479	14
12	15.46410162	15
13	16.60555128	17
14	17.74165739	18
15	18.87298335	19
16	20	20
17	21.12310563	21
18	22.24264069	22
19	23.35889894	23
20	24.47213595	24
21	25.58257569	26
22	26.69041576	27
23	27.79583152	28
24	28.89897949	29
25	30	30
26	31.09901951	31
27	32.19615242	32
28	33.29150262	33
29	34.38516481	34
30	35.47722558	35
31	36.56776436	37
32	37.65685425	38
33	38.74456265	39

We see that the square numbers 4, 9, 16, 25 and 36 are indeed missing from this table.

Why should this be so?

I am going to use an argument due to David Ratcliffe (@daveinstpaul)Â that splits into two different cases and uses an argument by contradiction, which is part of a series of techniques that mathematicians use that go by the general name of “counterfactuals”.

Terry Tao has written extensively about these sort of arguments, The general idea is that we set up a world that we believe cannot exist – sort of like in science fiction, but math fiction. Then we carefully examine this world for consequences and see if something truly unacceptable occurs. If it does, we conclude that no such world can exist.

The world we set up is one in which, contrary to our empirical observations, there is an instance of a positive integer $n$ for which rounding $n+\sqrt{n}$ to the nearest integer gives us a square number, which we will name $k^2$ .

What does rounding $n+\sqrt{n}$ to get $k^2$ mean, in a way that allows us to think about consequences?

It means that $k^2-\frac{1}{2}< n+\sqrt{n} < k^2+\frac{1}{2}$ .

How can we use this imaginary scenario to draw conclusions, hopefully very strange ones?

Let’s think about the following two mutually exclusive cases, at least one of which must hold good:

$n\leq k^2-k$ .

In this case imagine, counterfactually, that $\sqrt{n}\geq k-\frac{1}{2}$ .

Then $n \geq (k-\frac{1}{2})^2=k^2-k+\frac{1}{4}> k^2-k$ .

This contradictory state of affairs means that, in this case, we have $\sqrt{n}<k-\frac{1}{2}$ .

Then $n+\sqrt{n}< (k^2-k)+(k-\frac{1}{2})=k^2-\frac{1}{2}$

2. $n > k^2-k$ .

In this case, because $n$ is an integer, we have $n\geq k^2-k+1$ .

In this case, imagine, again counterfactually, that $\sqrt{n}\leq k-\frac{1}{2}$ .

Then $n \leq (k-\frac{1}{2})^2=k^2-k+\frac{1}{4}$ , contrary to $n \geq k^2-k+1$ .

Again, this contradictory state of affairs means that, in this case, we have $\sqrt{n}>k-\frac{1}{2}$ .

Then $n+\sqrt{n}> (k^2-k+1)+(k-\frac{1}{2})=k^2+\frac{1}{2}$ .

In either case, $n+\sqrt{n}$ does not lie between $k^2-\frac{1}{2}\textrm{ and } k^2+\frac{1}{2}$ as we assumed counterfactually.

This contradictory state of affairs means that, contrary to what we asserted in our counterfactual world, we can never round $n+\sqrt{n}$ to obtain the square of an integer.