What is a triangle? The role of definition
Posted by: Gary Ernest Davis on: October 2, 2010
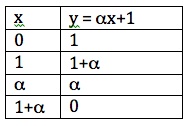
The Galois field of order 4 is the set with addition and multiplication given by the following tables:
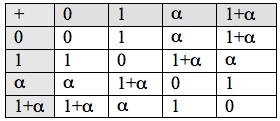
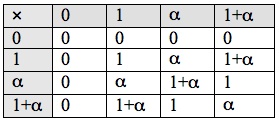 Because
Because for every
we see that not only addition and multiplication, but also subtraction is always possible in GF(4), although subtraction is trivial since
.
Also, because we see division, except by 0, is always possible in GF(4). This makes GF(4) an example of a mathematical field, one of the finite fields discovered by Evariste Galois who died at age 20.
We can use the finite field GF(4) , much as we use the real numbers, to construct a plane , which in this case is a finite plane:
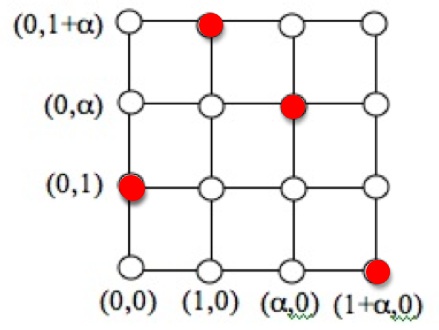
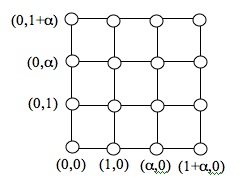 In this plane we can construct a line, much as we can in the Euclidean plane. For example the line
In this plane we can construct a line, much as we can in the Euclidean plane. For example the line contains points as follows:
and so looks like this in the plane :
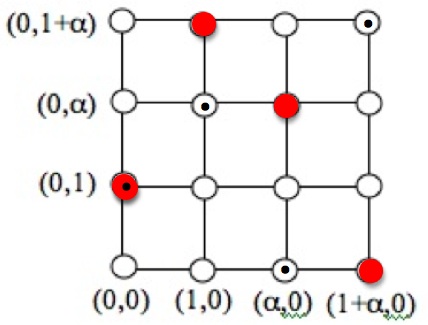
Now let’s try to build a triangle by producing a line from the point with slope
. This will be a line with equation
passing through the point
, so
. The points on the line
are given as follows:
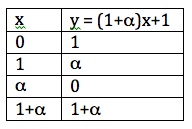 and this looks as follows in the plane
and this looks as follows in the plane (shown with dots):
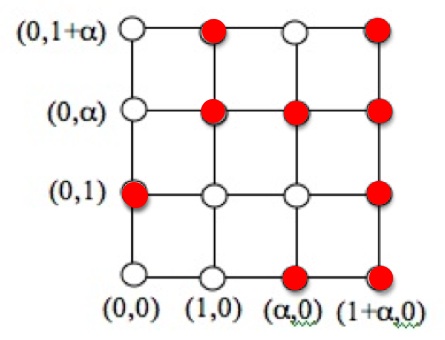
Now let us complete a triangle by joining the point to the point
by a line. A line which does this has equation
. So filling in all the points on the lines constituting the triangle, we get:
This triangle is determined by 3 lines, each with 4 points. The lines meet at 3 endpoints, leaving two other points on each line to form the triangle.
Such is the nature of mathematicians that they give the same name to different looking, but similarly defined objects. It is the definition, and not the appearance, that determines what sort of object we have.
The understanding of finite fields to construct this simple example, and much, much more, was made possible through the work of the incomparable Evariste Galois.
4 Responses to "What is a triangle? The role of definition"
A Guide to Basic Billiards Equipment…
I found your entry interesting thus I’ve added a Trackback to it on my weblog :)…
LeMystereno97159 Lolita Underwire Triangle Bra…
I found your entry interesting thus I’ve added a Trackback link to it on my weblog :)…


October 3, 2010 at 8:27 pm
I get 1+α, not 0, for αx+1 with x=1. Am I wrong?
October 4, 2010 at 5:16 am
You are right, of course. Thanks for pointing this out. I made the correction.