Cantor's basic idea of infinity plus 1

Posted by: Gary Ernest Davis on: October 1, 2010

In: Uncategorized
Comment!

0 Shares

Georg Cantor

Many people do not think it is problematic to bundle all the counting numbers together in a set: the set of all natural numbers. Yet from a set-theory perspective this is an explicit axiom – the axiom of infinity – because the other axioms of what by now are standard set theories allow an interpretation with finite sets only. So we need an explicit axiom to ensure that the natural numbers can form a set. It’s common to denote this set by $\mathbb{N}$ , and people will get into ferocious, but unenlightening, debates about whether 0 is, or is not, in $\mathbb{N}$ . We will assume 0 is not in $\mathbb{N}$ and that $\mathbb{N}$ begins $\{ 1, 2, 3, \ldots\}$ .

Galileo noticed a peculiar thing about this infinite set of all natural numbers – that it can be placed into one-to-one correspondence with a smaller part of itself:

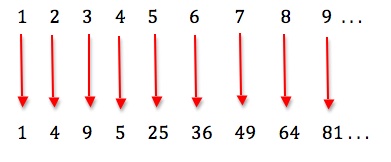Galileo reasoned that the squares of whole numbers are themselves whole numbers, but only a part thereof – for example 3 is not the square of a whole number. Yet the squares are matched to all whole numbers by the reverse operation of taking the square root.

Because one-to-one correspondence is the basis of how we count, to answer the question “How many?”, Galileo’s observation is that there are, from this perspective, just as many squares of whole numbers as there are whole numbers. Similarly, there are just as many even numbers as there are whole numbers:

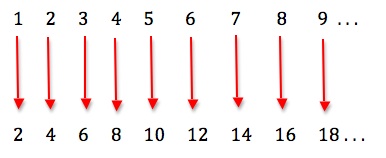This is a peculiarity of an infinite set: it can be placed into one-to-one correspondence with a part of itself, quite unlike the situation for finite sets.

Cantor was aware that even if we were to enlarge the set of natural numbers by putting in a new element, we would essentially still have he same number of elements. What new element could we add to the set $\mathbb{N}$ ? What about $\mathbb{N}$ itself?

We’ve added $\mathbb{N}$ to the right of all the natural numbers to indicate that we regard this new element as bigger than any natural number.

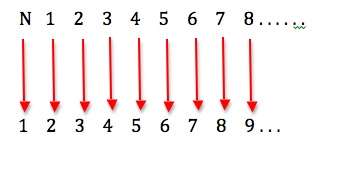
But still we can match this new enlarged infinite set one-to-one with the set of natural numbers:

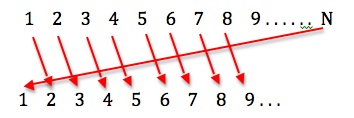Any infinite set that can be matched in one-to-one correspondence with the natural numbers is called a countably infinite set, and the cardinality – or counting size – of a countably infinite set is denoted by $\aleph_{0}$ .

“ $\aleph_0$ green bottles, hanging on the wall,

$\aleph_0$ green bottles, hanging on the wall,

If one green bottle should accidentally fall,

There’d be $\aleph_0$ green bottles, hanging on the wall.

“ $\aleph_0$ green bottles, hanging on the wall,

$\aleph_0$ green bottles, hanging on the wall,

If two green battles should accidentally fall,

There’d be $\aleph_0$ green bottles, hanging on the wall.

… …”

The one-to-one matching above does not preserve the order of all the elements. For example $1<\mathbb{N}$ by our choice of where we placed the new element $\mathbb{N}$ but in the one-to-one correspondence, 1 is matched with 2, $\mathbb{N}$ is matched with 1, but 2 > 1.

If you think about it a bit you can see that no matter what we match $\mathbb{N}$ with, we cannot preserve the order of the set $\{1, 2, 3, \ldots \mathbb{N}\}$ .

So the set $\{1, 2, 3, \ldots \mathbb{N}\}$ cannot be matched in a one-to-one correspondence with the set $\mathbb{N}$ so as to preserve order.

One-to-one matchings that preserve order give us a new way of thinking about “How many?”

Infinite ordered sets that can be matched in a one-to-one order preserving way are said to have the same ordinality as $\mathbb{N}$ and this ordinality is denoted by $\omega$ .

From an order perspective the ordered set $\{1, 2, 3, \ldots \mathbb{N}\}$ is bigger than the ordered set $\mathbb{N}$ , and it is natural to denote its ordinality by $\omega + 1$ .

On the other hand, if we think about what $1+\omega$ would be, it would be the ordinality of the set $\{ \mathbb{N}, 1, 2, 3, \ldots\}$ and this set CAN be matched in a one-to-one order preserving way with $\mathbb{N}$ :