Astonishing consequences of naive thinking about sets: Cantor's diagonal argument
Posted by: Gary Ernest Davis on: October 4, 2010
I have mentioned in several posts now that many people do not think it is problematic to bundle all the counting numbers together in a set: the set of all natural numbers, denoted .
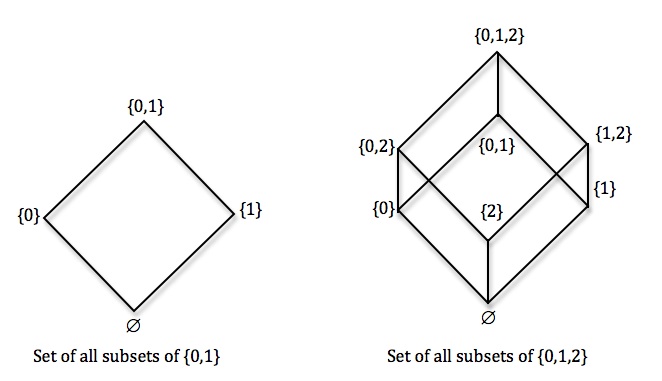
Another apparently harmless naive thought about set formation is that one can always construct the set of all subsets of a given set. For a set the set of all subsets of
is denoted by
. For simple sets such as
we can easily visualize
and the relations between its elements – i.e. the subsets of
:
where denotes the empty set, and rising lines indicate the set below is a subset of the set above.
Perhaps someone might balk at reflecting on a set consisting of all subsets of the natural numbers, yet there is a simple device to make this construction seem plausible.
The set of all subsets of a set
is in one-to-one correspondence with the set of all functions from the set
into the two element set
.
This correspondence is established as follows: for each subset define a function
by
; conversely, for each function
define a subset
of
by
.
So to think about all subsets of the set of natural numbers, it is equivalent, to think about all functions
.
Such functions give a value of for each natural number, and so correspond to sequences
where each
is either
.
Georg Cantor established the following extremely simple, yet devastating, result: for any set for which the set
of all subsets of
exists, there cannot be a one-to-one correspondence between
and
.
The argument is incredibly simple as it is elegant.
A one-to-one correspondence between and
is established by a function
that is invertible. Cantor shows that no function
is invertible. Here’s how he does it: let
be a function. Define the subset
by
. Then, for every
exactly when
. Because either
for every
it follows that
for all
, and therefore the function
is not invertible.
This is Cantor’s famous diagonal argument. Quite simple and relatively uncontroversial. Yet is has a devastating and astonishing consequence.
Given that, naively, we can always form the set of all subsets of a set
, we see that the set
of all subsets of natural numbers cannot be put into one-to-one correspondence with
itself. Because the mapping
from
is one-to-one, but not invertible, the set
has greater cardinality than that of
. That is, the set of all subsets of natural numbers is a set of greater order of infinity than the set of natural numbers itself.
What now stops us from forming the set which, by Cantor’s argument, has a higher order of infinity again, and so on, and so on(ad infinitum and beyond …) ? This is a glimpse of Cantor’s paradise from which, David Hilbert averred, no one shall expel us.

October 4, 2010 at 10:27 am
Great post.