Some stubborn problems associated with the number 3/2

Posted by: Gary Ernest Davis on: December 4, 2010

In: Uncategorized
Comment!

0 Shares

Fractional parts of powers of 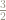$\frac{3}{2}$

The powers of $\frac{3}{2}$ increase exponentially:

However, if we keep only the fractional part of $(\frac{3}{2})^n$ – that is, $(\frac{3}{2})^n-Floor[(\frac{3}{2})^n]$ – quite a different picture results:

The first few of these numbers are 1/2, 1/4, 3/8, 1/16, 19/32, 25/64, 11/128, 161/256, 227/512, 681/1024, 1019/2048, 3057/4096.

Despite much study, there are things about this sequence of fractional numbers that are not known.

Equidistribution

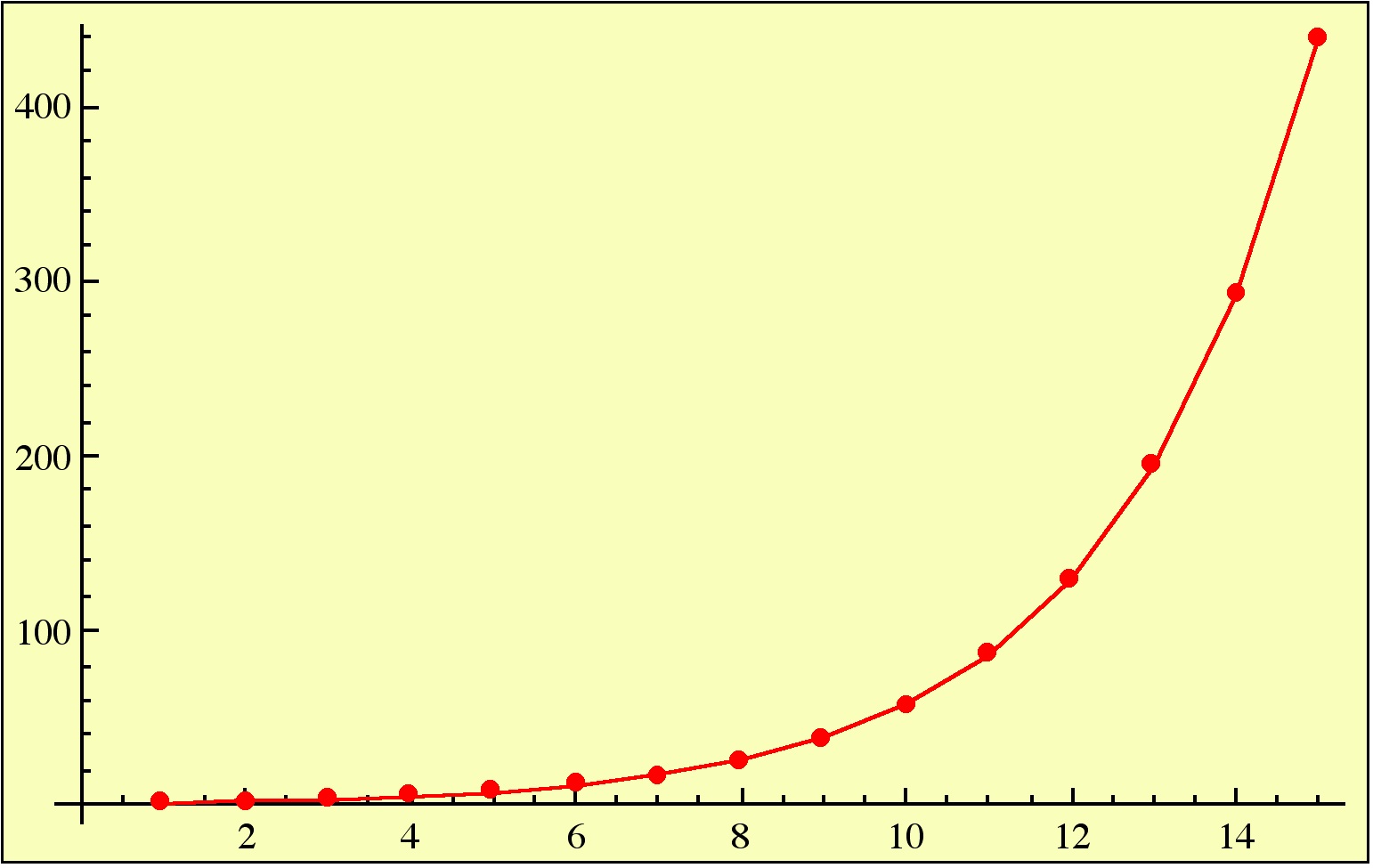
If we take an interval of numbers such as $[0.2, 0.3]$ and for each $n\geq 1$ count how many times $(\frac{3}{2})^n$ lies between $0.2 \textrm{ and } 0.3$ , will the ratio of the number of times to $n$ approach the length of this interval – namely, 0.1 – as $n$ increases?

For example, in the second picture above, it is true that for exactly 101 values of $n$ we have $0.2\leq (\frac{3}{2})^n\leq 0.3$ , and $\frac{101}{1000} =0.101\approx 0.1$ .

This property, when true for any interval $[a,b]\textrm{ with } 0\leq a < b\leq 1$ is known as equidistribution of the sequence of numbers $(\frac{3}{2})^n$ .

Back in 1914 Hardy & LittlewoodÂ proved that for “most” numbers $x$ the numbers $x^n-Floor[x^n]$ are equidistributed in the interval $[0,1]$ .

(Hardy, G.Â H. and Littlewood, J.Â E. “Some Problems of Diophantine Approximation.” Acta Math. 37, 193-239, 1914)

Godfrey Hardy and John Littlewood

It is not known if $x=\frac{3}{2}$ is one of those numbers.

Density

An equidistributed sequence of numbers $0\leq x_n\leq 1$ must land in every interval $[a,b] \textrm{ with } 0\leq a < b\leq 1$ because the $x_n$ must land in $[a,b]$ the right number of times.

The property of landing in each interval $[a,b]$ at least once is called density of the sequence $x_n$ .

It is not even known if the sequence $(\frac{3}{2})^n$ is dense, let alone whether it is equidistributed.

A powerful, but stubborn, inequality

It is widely believed, but still not known, if the fractional part of $(\frac{3}{2})^n$ , namely $(\frac{3}{2})^n-Floor[(\frac{3}{2})^n]$ , satisfies the inequality:

$(\frac{3}{2})^n-Floor[(\frac{3}{2})^n] \leq 1-(\frac{3}{4})^n$ for all $n\geq 1$ ………………..(*)

If this inequality is true then a famous problem of number theory – Waring’s problem – is known to be true.

The inequality (*) seems innocent enough, yet no-one to date has been able to prove it is true.

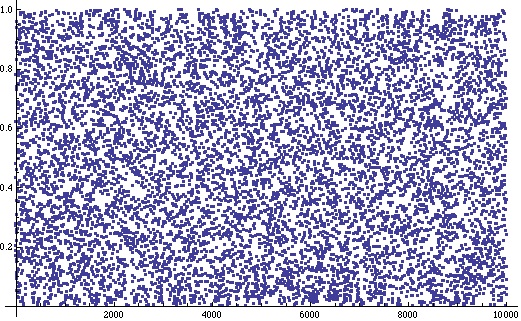
If (*) is true and we plot $F(n):=1-(\frac{3}{4})^n -((\frac{3}{2})^n-Floor[(\frac{3}{2})^n])$ versus $n$ we should never get a negative value.

A plot of the first 10,000 of these numbers $F(n)$ looks as follows:

Of course it’s hard to see from this plot how close to 0 the values of $F(n)$ get.

There are values of $n$ for which $F(n)$ is smaller than $F(i)$ for all previous $i$ .

The first few of these values of $n$ and the corresponding values of $F(n)$ are:

Values of n for which F(n) is less than any previous F(i)	F(n)
5	0.168945
14	0.0529218
46	0.0317909
58	0.0297681
105	0.0144072
157	0.00725365
163	0.00449855
455	0.00314395
1060	0.00110873
1256	0.000564205
2677	0.000363945
8093	0.0000809868
28277	0.0000604566
33327	0.0000549506
49304	0.00000736405

Is this a “good” problem?

The inequality (*) is intriguing, and if you can prove it you will undoubtedly become (mathematically) famous.

But it is it a good problem to work on?

A graduate student should not work on this problem because the chances of getting anywhere new are very slim.

A professional mathematician might play with it, in the hope of having a few ideas.

School students might also play with it in the hope of getting a sense of what the problem means and why it is hard: there are very few such hard problems in mathematics, with such strong implications, that are so easily stated.

A good starting point for school students to experiment is with the the fractional part of the powers of $\frac{1+\sqrt{5}}{2}$ .

Republic of Mathematics blog