Some curly questions on the base 3 digits of powers of 2
Posted by: Gary Ernest Davis on: December 6, 2010
Representing positive integers base 3
Positive whole numbers can easily be written in base 3, there where we allow the digits 0, 1, 2
For example: which we write as
, where the notation picks out the digits
and puts a subscript “3” to remind us that these digits need to be multiplied by appropriate powers of 3 and then added.
Using this notation and
because
Base 3 digits of powers of 2
How do the base 3 representations of powers of 2 look?
Here are the base 3 digits of the first 50 powers of 2:
| n | Base 3 digits of |
| 0 | 1 |
| 1 | 2 |
| 2 | 11 |
| 3 | 22 |
| 4 | 121 |
| 5 | 1012 |
| 6 | 2101 |
| 7 | 11202 |
| 8 | 100111 |
| 9 | 200222 |
| 10 | 1101221 |
| 11 | 2210212 |
| 12 | 12121201 |
| 13 | 102020102 |
| 14 | 211110211 |
| 15 | 1122221122 |
| 16 | 10022220021 |
| 17 | 20122210112 |
| 18 | 111022121001 |
| 19 | 222122012002 |
| 20 | 1222021101011 |
| 21 | 10221112202022 |
| 22 | 21220002111121 |
| 23 | 120210012000012 |
| 24 | 1011120101000101 |
| 25 | 2100010202000202 |
| 26 | 11200021111001111 |
| 27 | 100100112222002222 |
| 28 | 200201002221012221 |
| 29 | 1101102012212102212 |
| 30 | 2202211102201212201 |
| 31 | 12112122212110202102 |
| 32 | 102002022201221111211 |
| 33 | 211011122110220000122 |
| 34 | 1122100021221210001021 |
| 35 | 10021200120220120002112 |
| 36 | 20120101011211010012001 |
| 37 | 111010202100122020101002 |
| 38 | 222021111201021110202011 |
| 39 | 1221120000102112221111022 |
| 40 | 10220010000212002212222121 |
| 41 | 21210020001201012202222012 |
| 42 | 120120110010102102112221101 |
| 43 | 1011010220020211212002212202 |
| 44 | 2022021210111200201012202111 |
| 45 | 11121120121000101102102111222 |
| 46 | 100020011012000202211212000221 |
| 47 | 200110022101001112200201001212 |
| 48 | 1100220121202010002101102010201 |
| 49 | 2201211020111020011202211021102 |
x
How do the numbers of base 3 digits of vary with
?
Below are plots of the number of occurrences of digits 0, 1, 2 in the base 3 representation of for
:
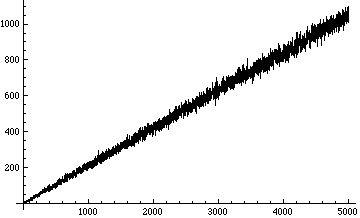
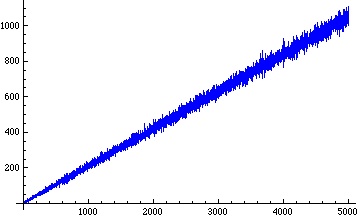
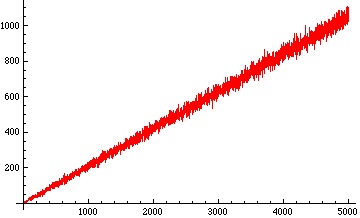
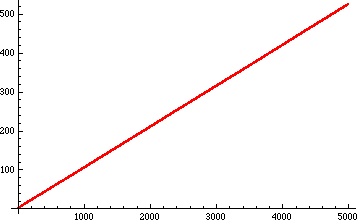
When we plot the running average of the number of occurrences of the digit 2 in the base 3 representation of – that is, the average of the numbers in the third (red) plot above from the very beginning – we get a remarkably straight line:
Erdös conjecture on the digit 2
Paul Erdös noticed that the base 3 representation of contains no 2 digit, but that after that the base 3 representation of powers of 2 seem to always contain the digit 2. He conjectured this is so, and to this day no-one knows whether this is true or not.
If we look again we see that in this list the base 3 representation of contains the digit 2 twice, and that seems to be true for the other powers
with
Put another way, seems it might be the last integer for which the base 3 representation of
contains just one occurrence of the digit 2, just as
seems to be the last integer for which the base 3 representation of
contains no occurrences of the digit 2.
We can carry out a search for those integers that are the last integer for which the base 3 representation of
contains
 or less occurrences of the digit 2.
The search reported below was restricted to .
| k | N(k) = largest n such that |
| 0 | 8 |
| 1 | 24 |
| 2 | 26 |
| 3 | 26 |
| 4 | 36 |
| 5 | 36 |
| 6 | 37 |
| 7 | 42 |
| 8 | 48 |
| 9 | 54 |
| 10 | 76 |
| 11 | 76 |
| 12 | 76 |
| 13 | 76 |
| 14 | 76 |
| 15 | 78 |
| 16 | 110 |
| 17 | 111 |
| 18 | 121 |
| 19 | 134 |
| 20 | 134 |
Note that .
This means that for all integers the base 3 representation contains more than 2, and more than 3, occurrences of the digit 2.
As we can see from the first table above, when it seems that the base 3 representation of
contains at least 4 occurrences of the digit 2. This remains true in the range
.
A plot of the estimates of is shown below:
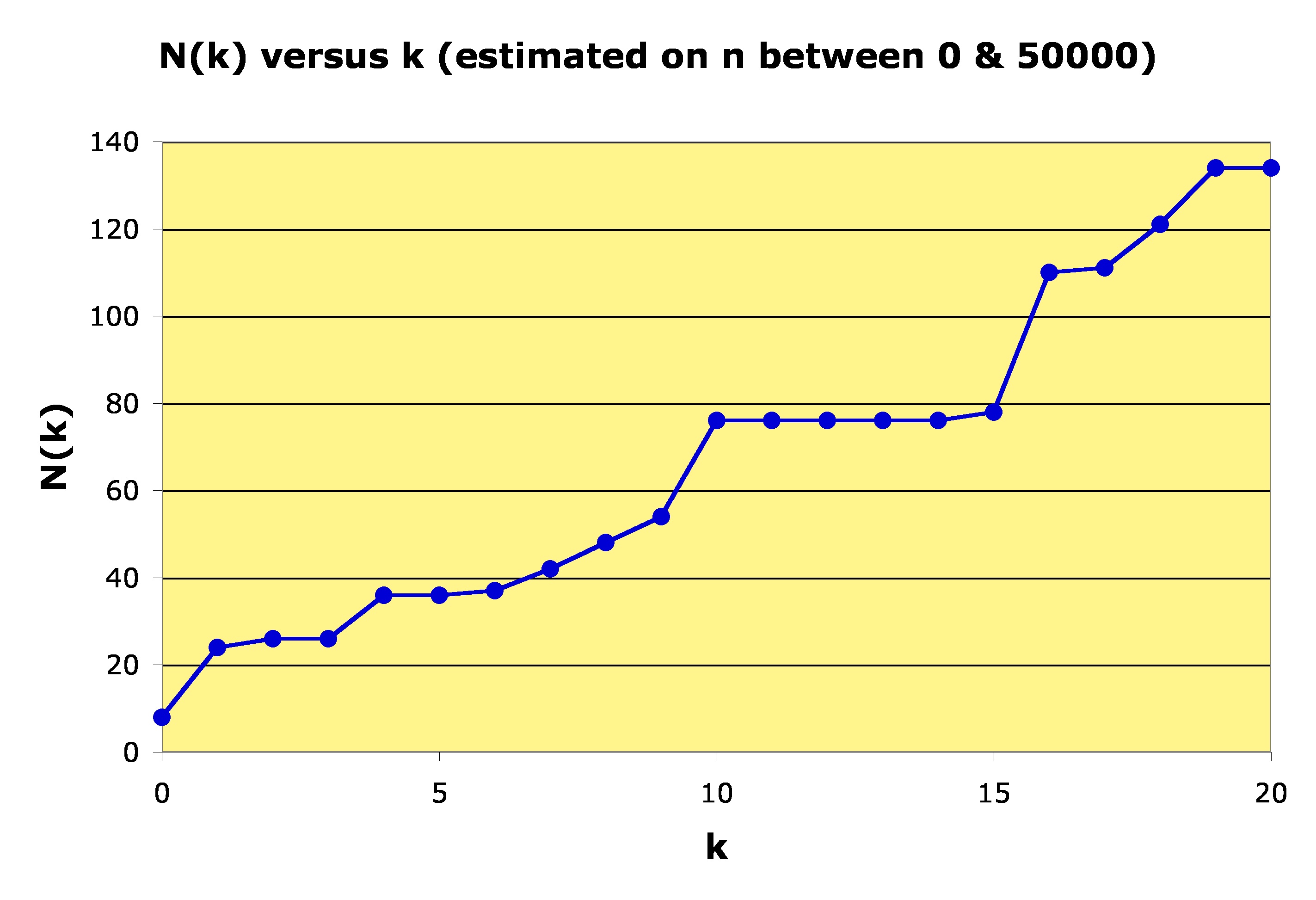 These are only estimates because we do not know for sure that further calculations for a larger range of
These are only estimates because we do not know for sure that further calculations for a larger range of might not change these values.
We do not have proofs for any of these estimates.
The occurrence and growth of the digits of in base 3 offer plenty of scope for experimentation by school students and undergraduate students of mathematics.
It seems we can obtain good guesses about the appearance of these digits, without yet knowing in any way how to prove any of these guesses.


December 6, 2010 at 1:12 pm
I wonder what happens with balanced ternary instead of ternary notation?
Or powers of other numbers, in other bases.
December 6, 2010 at 1:46 pm
Those are very good questions, Peter.
I think other powers and other bases give similar empirical results.