Why, exactly, is the square root of 2 not a rational number?
Posted by: Gary Ernest Davis on: December 3, 2010
Right angled triangles and 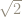
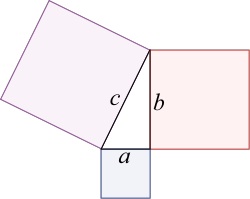
The Pythagorean theorem tells us that a square erected on the hypotenuse of a right-angled triangle will have an are equal to the sum of the areas of squares erected on the other two sides:
In particular, a right-angled triangle with the two sides adjacent to the right angle having length 1 will have a hypotenuse whose square is 2.
Pythagoras’ school of mathematics discovered that there is no ratio of whole numbers – or as we say nowadays, no rational number – whose square  is 2.
is 2.
This was shocking to the Pythagoreans because it showed that numbers, as they thought of them (whole numbers and ratios of whole numbers), could not measure all lengths. The reason this was shocking to them is that they assumed, as a matter of deep belief, that the numbers known to them could measure all known quantities.
So how can we see that is not a rational number?
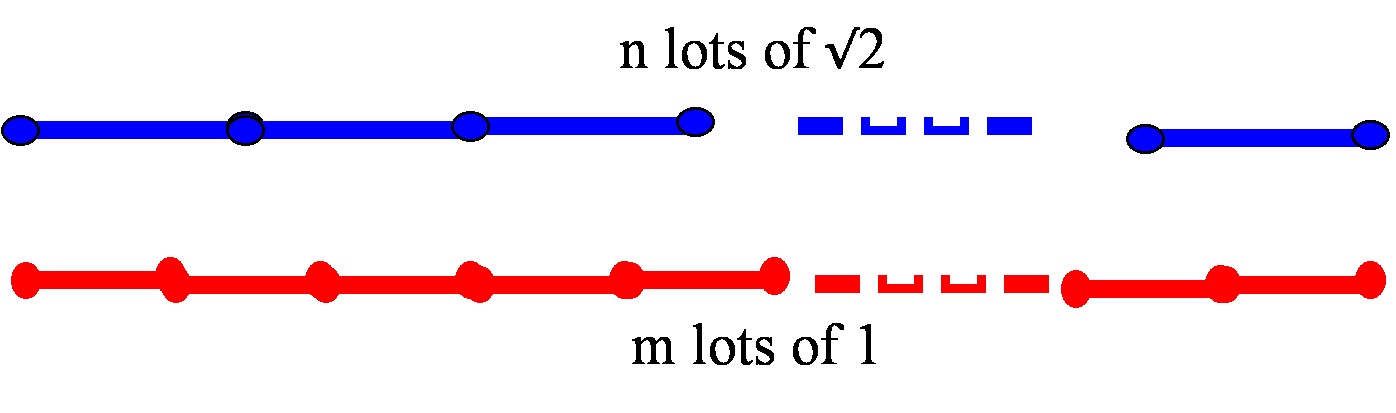
Let’s think about it the ancient Greek way: we will see that a line of length is not commensurable with a line of length 1.
By this we mean that if we step out a line of length a whole number of times the resulting length will never be the same as stepping out a line of length 1 any number of times:
How we see this is so is by stating a counterfactual situation: we enter an imaginary, potentially wholly fictitious, world in which it IS possible to exactly match a length that is a whole number multiple of with a length that is a whole number of multiples of 1:
The essence of the idea
Prior to a general argument let’s look at the basic idea in a manufactured, but illustrative, example.
Let’s imagine that .
We know this is, in fact, not quite right, because – not quite 2, but close.
Let’s just imagine, however, in a spirit of playfulness, that turned out to be exactly equal to 99.
In that case, let’s look at the number .
This number, , is a positive whole number less than 70, and we can check that:
In other words, we now have a situation where .
Now we can do this over again.
Let’s look at the number .
This new number, , is a positive whole number less than 29, and we can check that:
Now we have a situation where .
Well, you can see where we are heading; let’s do it again, with .
The number is again a positive whole number and it’s less than 29.
We can again check that is a positive whole number:
.
So now we have .
if we do this again we will get which is clearly not so.
So what? you may say. If we start with a falsehood , namely , and end up with a falsehood, namely
, what does this show?
Logically, it shows nothing, but it gives us the essence of a productive idea.
The productive idea is simply that:
if we ever have a positive whole number multiple of equal to a positive whole number then we can find smaller positive whole numbers that do the same job.
The general case
So imagine, that it is possible to match some whole number multiple of with some whole multiple of 1.
In other words, there are positive whole numbers such that
.
We will see that in this imaginary world we are lead to a contradictory state of affairs, from which we conclude that such an imaginary world does not exist.
There is a first occurrence of this phenomenon, by which we mean a smallest value of for which this happens.
Now lets look at the quantity .
First, because
. This is so because
.
Second, is a whole number because
.
Third, because
. This is so because
, since
.
Fourth,
In other words, we have found an earlier occurrence of a whole number multiple of that is a whole number multiple of 1, contrary to
being the first such occurrence.
This contradictory state of affairs means our imagined word does not exist, so a whole number multiple of can never be exactly equal to a whole number multiple of 1.
The short summary of the idea of this proof is as follows: if a positive whole number times
is a whole number, then the same is true for the smaller positive whole number
.
“Standard” proof by infinite descent
The commonly presented proof of the irrationality of is actually relatively complicated for students. When it is dissected as a structured proof one sees many subtle points in it such as knowing how and why a fraction can be written in its lowest terms (using Euclid’s algorithm). See here for more details.
Irrationality of other square roots
This is a follow up to a question from max@mathforum.
The essential point that makes the argument for the irrationality of work is that
.
Because of this fact, when we have a positive whole number n for which is also a positive whole number, then
is a positive whole number with the same property, and is less than n.
If we were to replace the number 2 by 5, for example, we would have to consider in order to get a number that is both positive and less than 1.
In general, for a non-square number p we use where
is the integer part of
.
Clearly this does not produce a positive number when p is a perfect square, so the technique breaks down then – as it should!
Cut The Knot
Alex Bogomolny has about 20 proofs that is not rational at his “Cut The Knot” site.
14 Responses to "Why, exactly, is the square root of 2 not a rational number?"
Aha. So when sqrt(n) – floor[sqrt(n)] the difference is 0 and p is not greater than n. This gives me more of an insight into why this proof works. Of course there’s a smallest value for n when the square root is rational: n = 1. When we imagine some rational number other than 1 that we could multiply irrational square roots by and get rational numbers, then weird things start to happen.
Does this line of reasoning also lead to a proof that if the product of an irrational number and another number is rational, that other number must have been irrational?
Max
Multiplying when
is not a square ensures that we get an number that is (a) positive and (b) less than n.
You say, “The commonly presented proof [by infinite descent] of the irrationality of √2 is actually relatively complicated.” However, G. H. Hardy gives this proof as one of examples of the simplest and beautiful “real” mathematics in his book “A Mathematician’s Apology” (p. 94 of Canto edition). Where does this difference come?
Thanks for the comment.
By Hardy’s standards it is simple. Most things were simple by his standards.
Yet this proof is notorious for the difficulties it causes students.
When the proof is analyzed structurally, as in the indicated link, one can see more clearly where the difficulties lie for students.
Hope this helps.
Do you mean the following? The “commonly presented proof” is based on the assumption that a rational number can be expressed by the ratio of positive integers that have no common factors. In order to prove this assumption, we need further procedure. Therefore, the total process of the “commonly presented proof” is relatively complicated compared with the one you presented.
The relative complexity of the two proofs can be followed by examining the structured hypertext proofs at http://www.crme.soton.ac.uk/research/proof/index.html
A structured proof often reveals hidden assumptions and complexities.
The empirically observed cognitive load for a student in the commonly presented proof of the irrationality of may be due to hidden complexity.
I do not know of any empirical studies with students that compare and contrast these two methods of proof.
Thanks; I see. Clicking the links in each of the Pythagorean proof and “Dedekind’s proof on the Web page you mentioned, we find that the former has more number of hidden assumptions. Only when we don’t care about most of those assumptions as if those were axioms, we would think that the former was simpler.
Dear Tabata Sensei,
yes, that is the idea I was trying to get across. Thank you for taking the time to dig into this. I very much appreciate your thoughts and comments.
I never had learned the proof by infinite descent. Rather, this was the proof I learned.
assume: m = sqrt (2) * n. Without loss of generality, you can assume that m and n have no factors in common. We’ll break down m into its prime factorization (2^m1)*(3^m2)*(5^m3)… and (2^n1)*(3^n2)… note that if n1 != 0 then m1 must be zero and vice versa.
square both sides. (2^2m1)*(3^2m2)*(5^2m3)…=(2^(2p1+1))*(3^2p2)… The fundamental theorem of arithmetic says that these decompositions are unique, so:
2m1 = 2p1 + 1. This is an impossible situation since 2m1 and 2p1 must both be even. Nice thing is this is very, very generalizable to both the statement “any non-integral square root must be irrational” as well as to cube roots, fourth roots, etc.
keep in mind that sqrt(2) is “rational” in certain fields, for example (mod 7) where sqrt(2) = 3.
Hi, thanks for this.
As for the proof by infinite descent, this proof also relies on being able to assume m and n have no common factors, and when we ask how do we know that this is true, we find it relies on Euclid’s algorithm.
This point – of why we assume no common factors – is a usual sticking point for many students.
Additionally, this proof uses the fundamental theorem of arithmetic, which is already more complicated than the proof in the post that is irrational.
There are two questions here: (1) which proof is simpler from a structured proof perspective? and (2) which proof is easier for students to comprehend?
Additionally, this proof uses the fundamental theorem of arithmetic, which is already more complicated than the proof in the post that is irrational.
It’s true that the proof of FTA is quite involved, but it is very much a ‘duh’ concept.
It was certainly a ‘duh’ concept for the mathematicians who thought they had proved Fermat’s Last Theorem by applying unique factorization in number fields where in fact it does not hold. There is, in fact, nothing obvious about prime factorization and unique prime factorization, and Hardy and Wright detail a couple of proofs of it in their book on number theory.

December 3, 2010 at 1:19 pm
This got me wondering: does the same exact argument work to prove that sqrt(3) is irrational and sqrt(4) is rational? Answer: it works for sqrt(3) since [sqrt(3) – 1] 3 are rational or irrational, right?
Will the more traditional argument work for testing the rationality of any integer?
Max
December 3, 2010 at 1:26 pm
Max, the same argument works to show that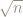 is irrational so long as n is not a perfect square, provided we consider
is irrational so long as n is not a perfect square, provided we consider ![\sqrt{n}-Floor[\sqrt{n}]](http://s0.wp.com/latex.php?latex=%5Csqrt%7Bn%7D-Floor%5B%5Csqrt%7Bn%7D%5D&bg=ffffff&fg=8E8778&s=0&c=20201002) .
.
This has to be positive for the argument to work. Clearly that fails if n is a square, such as n=4.