How do you find a power of 2 that begins with a 9?

Posted by: Gary Ernest Davis on: November 13, 2010

In: Uncategorized
Comment!

0 Shares

The problem of finding a power of 2 that begins with a 9 was posed in the recent #mathjams conference in the UK.

I tweeted:

republicofmath 2^n begins with 9 for n = 53, 63, 73, 83, 93, 156, 166, 176, 186, 249, 259, 269, 279, 289, 352, 362, 372, 382, 445, 455, 465 … #MathsJam

Following my tweet Barb Lynch asked:

Stelladuma @republicofmath How did you get the solutions for 2^n beginning with 9?

My answer was short and straight to the point (I had used Mathematica) but not explanatory:

republicofmath @Stelladuma 2^n beginning 9? #Mathematica: L = {}; Do[If[IntegerDigits[2^n][[1]] == 9, L = Append[L, n], L = L], {n, 1, 750}]; L #mathsjam

Barb Lynch, from Northeast Ohio, USA, is a teacher of algebra 1 and geometry to G/T middle school students. Chances are Barb does not have an available copy of Mathematica, and it’s highly likelyÂ her students do not have access to Mathematica even if she does.

So, if we are to adopt a computational solution to finding the powers of 2 that begin with 9, it would be handy to have another computational engine that students did have access to.

Enter a spreadsheet.

I will use Excel, but an open source spreadsheet, including that on Google Docs will do.

All we need from a spreadsheet is built-in functions for:

logarithms to the base 10
finding the whole number part of a decimal number
the ability to form powers.

All spreadsheets can do these things.

The idea is that we will generate a list of powers of 2 and examine that list to see which entries begin with a 9.

The one trick we need is to figure out how to extract the leading digit from a number such as “123′ when it is written in the spreadsheet.

Of course as human beings we just look to the left and speak the digit.

The question is: how do we instruct a spreadsheet to to do that?

The answer, it turns out, is surprisingly easy, using the miraculous powers of indices (otherwise known by the mysterious name of “logarithms”).

Here’s the idea:

To figure out how many powers of 10 are involved in a number such as 123, we take the logarithm, base 10, of the number. This makes sense because $log_{10}(10^k)=k$ . So, for example, $log_{10}(123) \approx 2.089905111$ .
To figure out what whole number of powers of 10 are involved in a number, such as 123 we drop the fractional bit of $log_{10}(123)=2.089905111$ to get 2. To do this in the spreadsheet we use the function “int” which takes the integer part of a decimal number.
Now we have now that 123 is in the range $10^2$ we need to divide by this number to figure how many of these powers of 10 we have. So we divide 123 by $10^2$ to get 1.23.
Now we are pretty much there: if we take the integer part of this number, using “int” we get 1. Voila! We have the leading digit of our number.

So here’s a how we might implement this in a spreadsheet (click on the image to enlarge it):

What do these spreadsheet formulas mean?

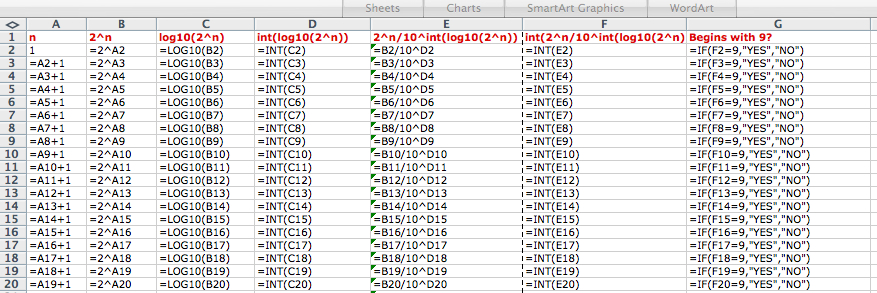
In the first column we are just creating a list of integers 1, 2, 3, 4, … by beginning with 1 and adding 1 at each step.
In the second column we are forming $2^n$ where n is the corresponding entry in the first column.
In the third column we are taking the logarithm, base 10, of the corresponding number in the second column.
In the fourth column we are finding the whole number part of the decimal number in the third column.
In the fifth column we are dividing the corresponding number in the second column ( $2^n$ ) by 10 raised to the power in the fourth column.
In the sixth column we are taking the whole number part of the decimal number in the fifth column.
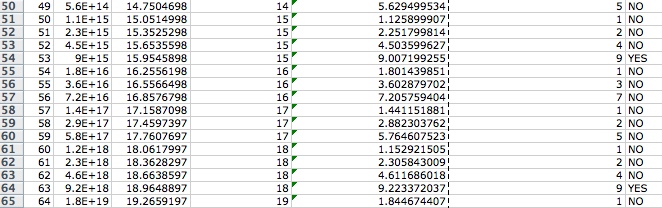
In the seventh column we asking the spreadsheet to say “YES” if the number in the sixth column is 9 (and “NO”otherwise)

When we do this without displaying formulas, ax I have done above, but just showingÂ numbers, we see that a “YES” first appears at n = 53, and another “YES” appears soon after at n = 63 (click on the image to enlarge it):

That’s it, from a computational perspective.

Pretty soon a spreadsheet will not be able to accurately calculate large powers of 2, so another computational engine needs to be used. That’s a story for another time.