How do you find a power of 2 that begins with a 9?
Posted by: Gary Ernest Davis on: November 13, 2010
The problem of finding a power of 2 that begins with a 9 was posed in the recent #mathjams conference in the UK.
I tweeted:
x
Following my tweet Barb Lynch asked:
- logarithms to the base 10
- finding the whole number part of a decimal number
- the ability to form powers.
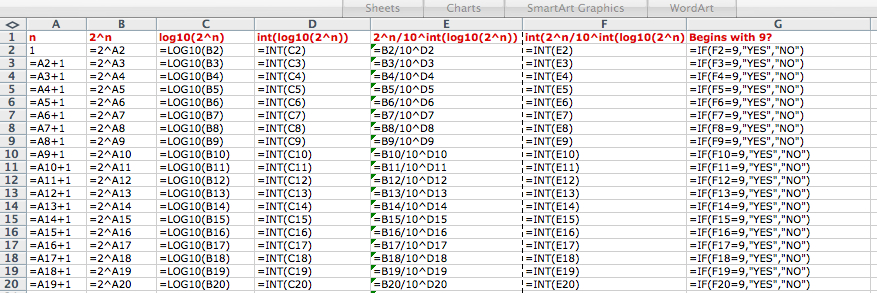
- To figure out how many powers of 10 are involved in a number such as 123, we take the logarithm, base 10, of the number. This makes sense because
. So, for example,
.
- To figure out what whole number of powers of 10 are involved in a number, such as 123 we drop the fractional bit of
to get 2. To do this in the spreadsheet we use the function “int” which takes the integer part of a decimal number.
- Now we have now that 123 is in the range
we need to divide by this number to figure how many of these powers of 10 we have. So we divide 123 by
to get 1.23.
- Now we are pretty much there: if we take the integer part of this number, using “int” we get 1. Voila! We have the leading digit of our number.
- In the first column we are just creating a list of integers 1, 2, 3, 4, … by beginning with 1 and adding 1 at each step.
- In the second column we are forming
where n is the corresponding entry in the first column.
- In the third column we are taking the logarithm, base 10, of the corresponding number in the second column.
- In the fourth column we are finding the whole number part of the decimal number in the third column.
- In the fifth column we are dividing the corresponding number in the second column (
) by 10 raised to the power in the fourth column.
- In the sixth column we are taking the whole number part of the decimal number in the fifth column.
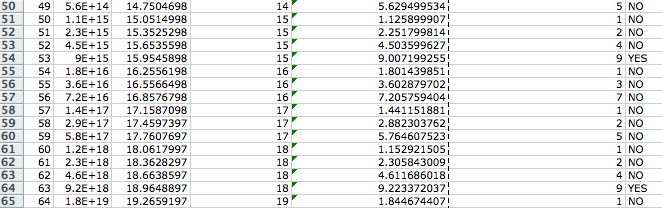
- In the seventh column we asking the spreadsheet to say “YES” if the number in the sixth column is 9 (and “NO”otherwise)
8 Responses to "How do you find a power of 2 that begins with a 9?"
Another fun observation is how many of those powers of 2 start with the digit 1: 30.1% of them in the long run. Then 17.6% start with 2, and so on. If you have a big slide rule around, you can show them the same proportions on the C or D scale. The same (first digit) thing works with our beloved Fibonacci numbers, and most any geometric sequence.
Dan have you blogged about this? Will you? Have you seen James Tanton’s YouTube video on Benford’s law?
You can also handle the larger powers of 2 by eliminating that column and only using the logarithms: n * log(2) rather than log(2^n). That ought to have sufficient accuracy at least up to 2^100000 or something in that neighborhood.
Here’s a solution in Python. Somewhat similar to the Mathematica solution, but Python is totally free and available to anyone.
>>> [n for n in range(1, 1001) if str(2**n)[0] == ‘9’]
[53, 63, 73, 83, 93, 156, 166, 176, 186, 249, 259, 269, 279, 289, 352, 362, 372, 382, 445, 455, 465, 475, 485, 548, 558, 568, 578, 641, 651, 661, 671, 734, 744, 754, 764, 774, 837, 847, 857, 867, 930, 940, 950, 960, 970]
Thanks for this Michel. I would very much like to get secondary mathematics teachers interested in using Python, particularly for computational explorations such as this.
Great post, thanks Michel for pointing me to this. I love seeing ways of using technology that imparts a valuable programming skill while giving students a deeper understanding of math (e.g. that 91 is 9*10+1).
I have blogged a bit about this here but I definitely need to give some more examples like this post.
http://brokenairplane.blogspot.com/2010/08/computer-science-programming-intro.html

November 13, 2010 at 4:55 pm
You can also do this without logarithms. Just multiply by 2 each time, and divide by 10 when the result exceeds 10. (This could be useful if students have not studied logarithms yet.)
November 13, 2010 at 5:01 pm
Thanks Dave. Always good to find a more direct, less complicated, way of doing things.