Area and “amount of stuff”

The area of a region is often colloquially thought of as the “amount of stuff” in that region.

This is not a good way of thinking about area because it leads to odd thinking such as the area of a region does not change if the perimeter changes “because the amount of stuff” hasn’t changed  – as if the boundary of the region contains “stuff” that is conserved as the shape of the boundary changes.

There is obviously something wrong with this “amount of stuff” model because a square of side lengths 1 cm has the same perimeter – 4 cm -  as a rectangle with side lengths , but the square has area 1 square cm, while the rectangle has area square cm.

Square and rectangle have the same perimeter. Each small square has area 1/4 square cm

So, the “amount of stuff” model of what’s inside a boundary leads to silly situations.

Conclusion? There is no “stuff” inside a boundary in the plane – that is, inside a closed non-intersecting figure drawn on a sheet of paper:

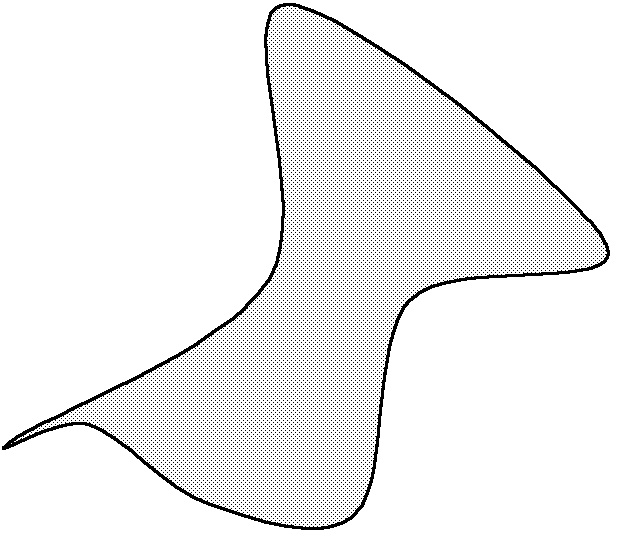
Contrary to appearances, there is no "stuff" inside this closed figure that is conserved as the shape of the boundary changes.

The area of a region therefore has nothing to do with any hypothetical “stuff” surrounded by the boundary of the region.

What then is the area of a region?

Part of the answer goes back to activities that teachers get children to do in the earliest grades – counting squares.

Many years ago when I was sitting in on a grade 2 class the teacher had the students draw objects on a gird of squares and asked them to count squares to estimate the area of the object they drew. I drew a robot that consisted of either rectangles of triangles (which are half rectangles). I did this because it would be easier to count squares if there weren’t any curvy bits to my figure. The children went “Ooh!’ when they saw my drawing, and of course, made me feel very clever!

This is a correct way of thinking about area: the number of unit sized tiles that it takes to exactly cover the figure, with no ties overlapping. For the children the grid squares were the unit tiles.

This way of thinking about area is a cognitive root: it is not the whole story about area, but it is easy for children to understand and does not have to be ditched when we learn more sophisticated notions of area.

Area of a circle

Some years ago, sitting with my friend and colleague Neil Pateman and a group of prospective teachers, in the sunshine at the University of Hawai’i at Manoa, one of the students said: “That’s what I don’t get. How do you measure a round circle in square inches?”

She was referring to the measurement of the area of a region bounded by a circle:

How many square tiles cover the circular region?

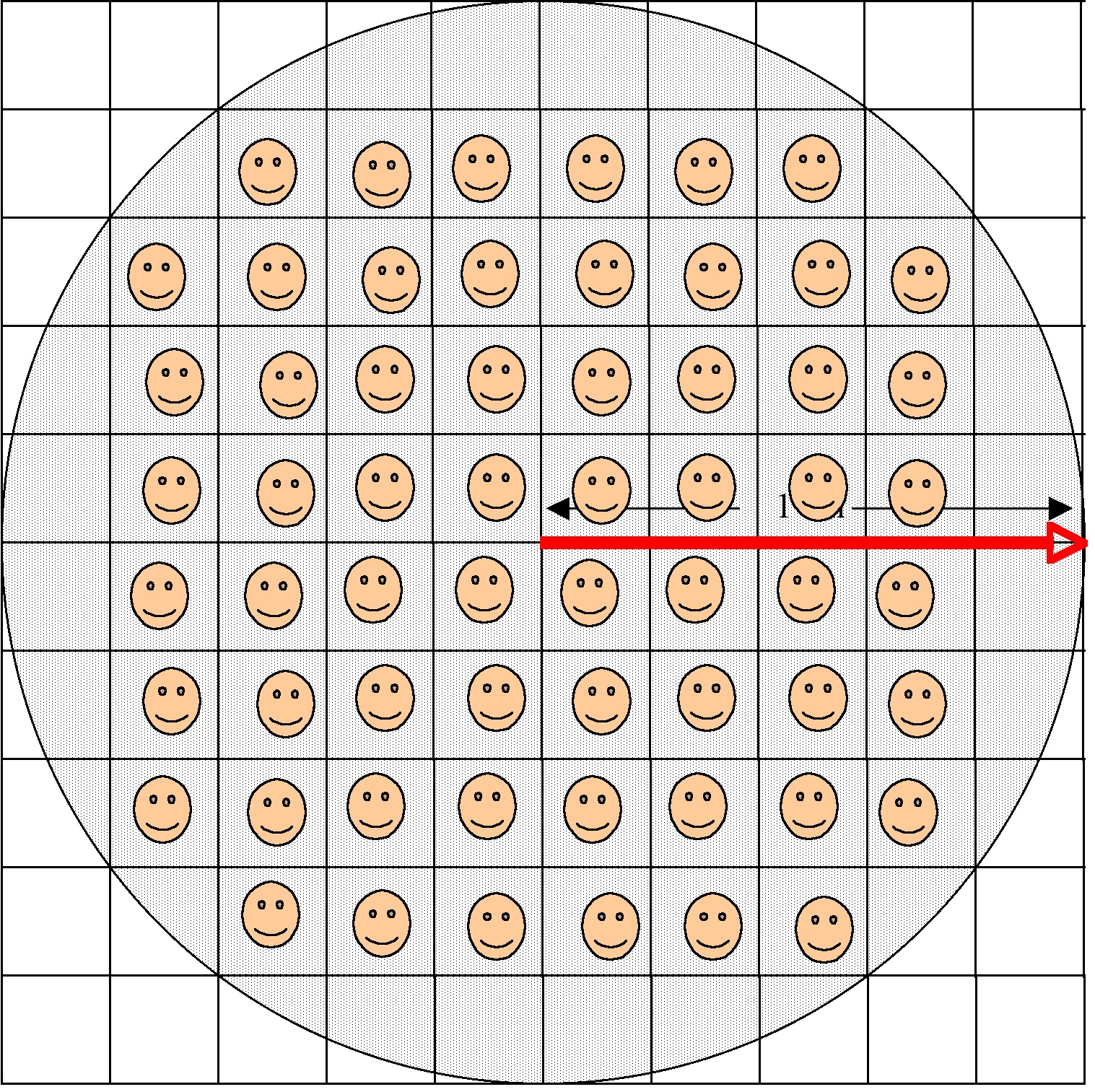
We can see that the question “How many square tiles cover the circular region?” does not have an exact whole number answer for the grid we have drawn.

It does not even seem to have an obvious fractional answer, due to the curvature of the circle as it passes over the grid lines.

Can we make an estimate of how many small tiles cover the circular region?

There are 60 small squares – those with smiley faces – that fit inside the circular region.

There are some other small squares – 28 of them – that contain either large or small pieces of the circular region.

So we know that 60 small squares lie inside the circular region, and 28 others overlap. Let’s estimate, roughly, that half of each these 28 other squares lies inside the circular region. This gives us an estimate of 60+28=88 small squares that either lie inside, or overlap by about half, the circular region.

What’s the area of these 88 small squares that lies inside the circular region?

With the radius of the circle shown as 1 cm, each small square has side length cm and therefore area square cm.

60 of these small squares lying inside, and 28 lying about halfway inside, the circular region gives us an area of square cm as an estimate for the area of the circular region.

This answer is not exact, because we made rough estimates.

Another way to estimate the area of the circular region would be to take the average of the area of the small squares lying inside it and the area of the large square containing it. This average is .

To get better estimates we could take a finer grid.

What is ?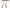

Because we can take finer and finer girds to estimate the area of a circular region it seems reasonable to assert that the circular region actually has an area.  In 1706, William Jones introduced a name, , for the ratio of the circumference of a circle to its diameter. This turns out to be the area of a unit circle, and the name stuck after it was popularized by Leonhard Euler.

This just a name, yet we have estimated that, roughly, – maybe a little bigger.

What then is really the value of ?

How might we try to answer this question?

One way would be to try to write as a fraction: for some whole numbers .

Unfortunately, this is not possible: is not a rational number.

This is not unlike which is also not a rational number.

Yet is even worse (or better, depending on your point of view): does not satisfy any polynomial equation with integer coefficients, unlike which satisfies .

Can we write as a decimal number?

Much effort has gone into this question.

begins 3.141592653589

As of September 26, 2010, Alexander J. Yee & Shigeru Kondo had calculated 5 trillion digits of – this was a new world record at that time.

The fact is that we do not know, and never will know the exact numerical value of – the exact spot that occupies on a number line.

We know a lot of other things about – a lot of its properties – but not its numerical value.

is a mysterious number – the mathematician Leopold Kronecker even denied there was such a number. For him, a quantity such as the area of a circle was not a number.