Happy mathematical new year: 2011 is the sum of 11 consecutive prime numbers
Posted by: Gary Ernest Davis on: January 1, 2011
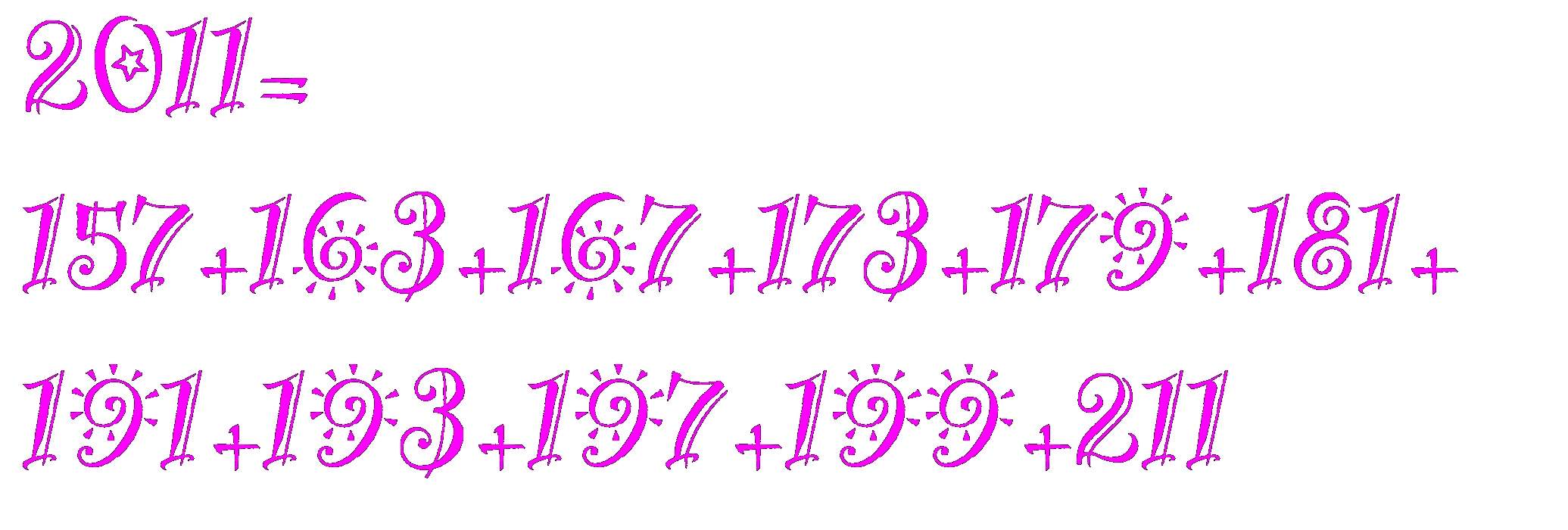xOn December 31, 2010 @mathematicsprof posted two interesting tweets:
@mathematicsprof 2011 is also the sum of 11 CONSECUTIVE prime numbers: 2011=157+163+167+173+179+181+191+193+197+199+211
x
Two prime numbers are “consecutive” if they follow one upon the other, in the collection of prime numbers. So, for example, 3 and 5 are consecutive prime numbers, as are 7 and 11.
These tweets, re-tweeted, attracted a fair amount of attention, deservedly so, because the second observation is both funny and thought provoking.
_____________________________________________________________________________________________________
Many people said to me they wished they had the “2011=157+163+167+173+179+181+191+193+197+199+211” on a T-shirt, so …. by popular demand I am happy to say that you can now purchase just such a T-shirt:
_____________________________________________________________________________________________________
I asked the question “Which prime numbers are sums of consecutive prime numbers” and David Radcliffe (@daveinstpaul) tweeted:
Primes expressible as the sum of consecutive primes: http://bit.ly/dKuh9S (2011 is an example!)
The link leads us to an entry in the On-Line Encyclopedia of Integer Sequencesâ„¢ in which there is some data on prime numbers that are sums of two or more consecutive prime numbers.
This On-Line Encyclopedia of Integer Sequencesâ„¢ entry includes Mathematica code to find such prime numbers.
The problem of finding prime numbers that are sums of two or more non-consecutive primes is a non-trivial computational exercise for school students and, it seems to me, one that many of them would find fun.
Here’s a variant of that problem, stemming from @mathematicsprof’s observation:
2011 is the sum of a prime number (11) of consecutive prime numbers.
Which prime numbers are a sum of a prime number of consecutive prime numbers?
Enjoy, and Happy New Year!
Postscript
The next year after 2010 that is a prime number and a sum of consecutive prime numbers is 2027 = 29+31+37+41+43+47+53+59+61+67+71+73+
79+83+89+97+101+103+107+109+113+127+131+137+139
but that year is not a sum of a prime number of consecutive prime numbers.
However, 2027 does have the curious and interesting property that it is prime and the sum of its digits 2+0+2+7=11 is also a prime number. It is the first year after 2003 that has this property.
The next year that is a prime number and a sum of a prime number of consecutive prime numbers is 2081 =401+409+419+421+431.
The following modification of Vladimir Orlovsky’s Mathematica code produces prime numbers that are a sum of a prime number of consecutive primes:
p = {};
Do[a = Table[Prime[i], {i, n, 100}];
l = Length[a];
k = 1;
While[Prime[k] < l + 1, b = Plus @@@ Partition[a, Prime[k]];
k++;
p = Append[p, Select[b, PrimeQ[#] &]]], {n, 1, 99}];
S =Union[Flatten[p]]
The first prime number that is a sum of two or more consecutive primes but is not a sum of a prime number of consecutive primes is 17 = 2+3+5+7
@mathematicsprof further tweeted on January 1, 2011:
2011 is also the sum of THREE consecutive primes 2011 = 661+673+677 . Can you write 2011 as the sum of 5, 7, 9, 11, 13, … primes?
This, of course, leads us to ask:
in how many ways can a prime number be written as a sum of consecutive primes?
(allowing, for convenience, a sum to have only 1 term, so that, for example 7 =7 can be written as sum of consecutive primes in only 1 way, whereas 5= 5 = 2+3 can be written as a sum of consecutive primes in 2 ways).
R packages that might be useful
People familiar with R might want to recode the above-mentioned Mathematica code in R.
Here are details of two packages that should prove useful in doing this:
Partitions: partitions
Primality checking: schoolmath
39 Responses to "Happy mathematical new year: 2011 is the sum of 11 consecutive prime numbers"
January 1, 2011 at 3:11 pm
That’s amazing! Not just prime, but the sum of so many consecutive primes. 2011, 157, and 11 are my new fav. primes. Actually commenting just to get follow-up comments, this has made my year! (In number only of course.)
January 2, 2011 at 12:07 pm
On average, roughly 70% of the natural numbers can be represented as a sum of consecutive primes in at least one way. This was proven by Moser in 1963.
So, there is about a 7 in 10 chance that any year from now on will be the sum of consecutive primes.
Also, there may be more than one way to write 2011 as a sum of consecutive primes.
Of course, New Year’s Day was 1/1/11, and 2011 is prime. Maybe the end of times is near.
January 2, 2011 at 2:28 pm
I tried to reproduce your results with R; my code (see below) does seem to produce the right results for 2011
2011 : 661 673 677
2011 : 157 163 167 173 179 181 191 193 197 199 211
Just as in the Mathematica example, I did create a list of consecutive prime numbers, and for each possible set of consecutive prime numbers from this list, I checked whether or not the sum is a prime number.
Checking all possible combinations doesn’t seem the most efficient way to solve this problem. Can this be done somehow more efficiently?
===================
#from stackoverflow.com/questions/3789968/generate-a-list-of-primes-in-r-up-to-a-certain-number
primes <- function(n){
primesR <- function(p, i = 1){
f <- p %% p[i] == 0 & p != p[i]
if (any(f)){
p <- primesR(p[!f], i+1)
}
p
}
primesR(2:n)
}
#from stackoverflow.com/questions/3789968/generate-a-list-of-primes-in-r-up-to-a-certain-number
isPrime <- function(x){
div <- 2:floor(sqrt(x))
!any(x %% div == 0)
}
#find all partitions of length n in x
partition<-function(x,n) {
N<-length(x);
lapply(seq(1,N-n+1,1),function(i) x[i:min(i+n-1,N)])
}
#find all partitions in x
partitions<-function(x) {
N<-length(x);
lapply(seq(1,N,1),function(i) partition(x,i))
}
#display only partitions where sum is prime
printPrimeSumOfPrimes<-function(x) {
N<-length(x);
for(i in 1:N) {
M<-length(x[[i]]);
for(j in 1:M) {
s <- sum(x[[i]][[j]]);
if(isPrime(s)) {
print(c(s,x[[i]][[j]]));
}
}
}
}
a <- primes(1000)
b <- partitions(a)
printPrimeSumOfPrimes(b)
January 3, 2011 at 8:07 pm
4603769 is the sum of 159 consecutive primes starting with 28151, the 3069th prime number. What do I win? Also, did I work that right? 28151 is the first prime that is the first in a sequence of more than a hundred to find a prime sum. Here’s my code:
# plot primes, by sequence, against how many additional ones must be
# added to it to get another.
#
# p1 is 2, and by adding p2, which is 3, to it, you get 5, so f(1) == 1.
# p2 is 3, 3+5 is 8, 8+7 is 15, 15+11 is 26, 26+13 is 39, …? how many
# will it take?
use strict; # good perl practice; default past 5.12
# here’s the Concise But Dumb Perl Prime Tester:
sub CBDisPrime($){
(‘A’x$_[0]) !~ m/^(AA+)\1+$/
}
#here’s a proper seive:
my @primes = (2,3,5); my $TooBig = 6;
sub isPrime{
my $x = shift;
$x % $_ or return 0 for @primes;
if($x > $TooBig){
my $top = 1+ int sqrt $x;
while ($TooBig++ 25;
1
};
# make it faster
use Memoize;
memoize(‘isPrime’);
# no partial lines in output
$| = 1;
# stop when we find one that takes a sequence of 100
my @lookahead = (3,5);
# loop over starter primes
my ($nn,$sum,@peas);
my $p = 1; my $n;
while(@lookahead “;
$sum = $n;
@peas = ($n);
# loop over sequential primes
findseq: {
for (@lookahead){
push @peas, $_;
$sum += $_;
isPrime($sum) and last findseq;
};
$nn = $lookahead[-1];
while(1){
isPrime(++$nn) or next;
push @lookahead, $nn;
push @peas, $nn;
$sum += $nn;
isPrime($sum) and last findseq;
};
};
BEGIN { $” = ‘, ‘ } # make a nice list
print @peas.”. Sum (@peas) == $sum\n”;
};
[…] Happy mathematical new year: 2011 is the sum of 11 consecutive prime numbers x […]
January 3, 2011 at 8:36 am
2+0+2+7=13 ???????
Wow!
January 3, 2011 at 10:07 am
LOL! Thanks Alexander. I didn’t spot that, and made the correction.
January 3, 2011 at 10:26 am
As 13 is my lucky number, I’ll note this about the new year day:
01 + 01 + 11 = 13
It’s going to be a very* good year.
January 3, 2011 at 12:45 pm
I’m excited about this prime event:
November 11th, 2011, sometime before lunch, which will be
11/11/11 11:11:11
Maybe we should use this to redefine “prime time”.
January 4, 2011 at 10:13 am
Nice, but you better ask Neon Deion first…
January 4, 2011 at 11:40 am
LOL. http://en.wikipedia.org/wiki/Deion_Sanders for those who didn’t get the reference.
January 17, 2011 at 12:09 pm
Also worth noting is that this would be the last binary datetime until 1 AM January 1, 2100 (1/1/00 1:00:00).
January 3, 2011 at 3:34 pm
Another interesting question might be how quantum computing methods could be applied to these searches.
January 3, 2011 at 5:30 pm
This would be a good topic for my MathCounts team this week.
January 3, 2011 at 8:12 pm
4603769 is the sum of 159 consecutive primes starting with 28151, the 3069th prime number. What do I win? Also, did I work that right? 28151 is the first prime that is the first in a sequence of more than a hundred to find a prime sum. Here’s my code:
# plot primes, by sequence, against how many additional ones must be
# added to it to get another.
#
# p1 is 2, and by adding p2, which is 3, to it, you get 5, so f(1) == 1.
# p2 is 3, 3+5 is 8, 8+7 is 15, 15+11 is 26, 26+13 is 39, …? how many
# will it take?
use strict; # good perl practice; default past 5.12
# here's the Concise But Dumb Perl Prime Tester:
sub CBDisPrime($){
('A'x$_[0]) !~ m/^(AA+)\1+$/
}
#here's a proper seive:
my @primes = (2,3,5); my $TooBig = 6;
sub isPrime{
my $x = shift;
$x % $_ or return 0 for @primes;
if($x > $TooBig){
my $top = 1+ int sqrt $x;
while ($TooBig++ <= $top ){
isPrime($TooBig) or next;
$x % $TooBig or return 0;
};
};
warn "$x is prime";
push @primes, $x;
# die "@primes" if @primes > 25;
1
};
# make it faster
use Memoize;
memoize('isPrime');
# no partial lines in output
$| = 1;
# stop when we find one that takes a sequence of 100
my @lookahead = (3,5);
# loop over starter primes
my ($nn,$sum,@peas);
my $p = 1; my $n;
while(@lookahead < 100){
warn @lookahead." entries in lookahead list\n";
$n = shift @lookahead; # isPrime(++$n) or next;
print $p++," ==> ";
$sum = $n;
@peas = ($n);
# loop over sequential primes
findseq: {
for (@lookahead){
push @peas, $_;
$sum += $_;
isPrime($sum) and last findseq;
};
$nn = $lookahead[-1];
while(1){
isPrime(++$nn) or next;
push @lookahead, $nn;
push @peas, $nn;
$sum += $nn;
isPrime($sum) and last findseq;
};
};
BEGIN { $" = ', ' } # make a nice list
print @peas.". Sum (@peas) == $sum\n";
};
January 4, 2011 at 5:19 pm
here is a more efficient sieve. The memoization is intrinsic, caching the found primes that are too large to append to the sieve list yet.
#here's a proper sieve:
my @primes = (2,3,5); my $TooBig = 5;my $counter;
sub isPrime{
my $x = shift;
# warn "q: $x p:[@primes] tb:$TooBig";
# die "debugging?" if ++$counter > 50;
my $top = 1+ int sqrt $x;
if ($top < $primes[-1]){
for (@primes){
$x % $_ or return 0;
$_ > $top and last
};
# warn "$x is prime, found no factors < $top in [@primes]";
return 1
};
# warn "$top is > $primes[-1]";
for (@primes){
$x % $_ or return 0;
};
# warn "will add to list now.";
if($x > $TooBig){
while ($TooBig <= $top ){
# warn "tb ( $TooBig ) LE $top";
isPrime(++$TooBig) or next;
push @primes, $TooBig;
warn "$TooBig is prime";
# warn "list now [@primes]";
$x % $TooBig or return 0;
};
warn "$x is too big for our sieve";
return 1;
};
die "IMPOSSIBLE";
};
# make it faster
use Memoize;
memoize('isPrime');
January 4, 2011 at 8:12 am
Hi,
I’m Gaurav Garg From http://www.Hackersfind.com
This post IS amazing. I like the one in 2011.
January 5, 2011 at 6:48 am
#from stackoverflow.com/questions/3789968/generate-a-list-of-primes-in-r-up-to-a-certain-number
primes <- function(n){
primesR <- function(p, i = 1){
f <- p %% p[i] == 0 & p != p[i]
if (any(f)){
p <- primesR(p[!f], i+1)
}
p
}
primesR(2:n)
}
#from stackoverflow.com/questions/3789968/generate-a-list-of-primes-in-r-up-to-a-certain-number
isPrime <- function(x){
div <- 2:floor(sqrt(x))
!any(x %% div == 0)
}
#find all partitions of length n in x
partition<-function(x,n) {
N<-length(x);
lapply(seq(1,N-n+1,1),function(i) x[i:min(i+n-1,N)])
}
#find all partitions in x
partitions<-function(x) {
N<-length(x);
lapply(seq(1,N,1),function(i) partition(x,i))
}
#display only partitions where sum is prime
printPrimeSumOfPrimes<-function(x) {
N<-length(x);
for(i in 1:N) {
M<-length(x[[i]]);
for(j in 1:M) {
s <- sum(x[[i]][[j]]);
if(isPrime(s)) {
print(c(s,x[[i]][[j]]));
}
}
}
}
a <- primes(1000)
b <- partitions(a)
printPrimeSumOfPrimes(b)
January 7, 2011 at 11:36 am
Just another Nice Post. I will keep up with this one. Nice Post mate and Happy 2011
January 7, 2011 at 2:28 pm
This whole conversation is way over my basic math head, but I love primes!
January 7, 2011 at 2:35 pm
Hey Cassandra,
let us know if there’s something you want to know, or that we could explain better. Great to hear from you!
January 8, 2011 at 10:16 am
Great observations! You may be interested in some other general numerical observations at numbersknack.wordpress.com
[…] Republic of Math blog follows the consecutive-prime inquiry further, with the observation that 2011 can also be […]
January 15, 2011 at 1:06 pm
nice………………………..
^_^b
http://pokemon-f.blogspot.com/2010/06/pokemon-character-pokemon-pikachu.html
January 18, 2011 at 2:25 pm
Beautiful, isn’t it? I must link it. Don’t worry, I will attribute.
[…] Loving and HatingMathematics.Gary Davis at the Republic of Mathematics has a fun article about the number 2011. Not only is 2011 prime but it is also the sum of 11consecutive prime numbers. […]
January 20, 2011 at 5:43 am
Checking all possible combinations doesn’t seem the most efficient way to solve this problem. Can this be done somehow more efficiently?
===================
#from stackoverflow.com/questions/3789968/generate-a-list-of-primes-in-r-up-to-a-certain-number
primes <- function(n){
primesR <- function(p, i = 1){
f <- p %% p[i] == 0 & p != p[i]
if (any(f)){
p <- primesR(p[!f], i+1)
}
p
}
primesR(2:n)
}
#from stackoverflow.com/questions/3789968/generate-a-list-of-primes-in-r-up-to-a-certain-number
isPrime <- function(x){
div <- 2:floor(sqrt(x))
!any(x %% div == 0)
}
#find all partitions of length n in x
partition<-function(x,n) {
N<-length(x);
lapply(seq(1,N-n+1,1),function(i) x[i:min(i+n-1,N)])
}
#find all partitions in x
partitions<-function(x) {
N<-length(x);
lapply(seq(1,N,1),function(i) partition(x,i))
}
#display only partitions where sum is prime
printPrimeSumOfPrimes<-function(x) {
N<-length(x);
for(i in 1:N) {
M<-length(x[[i]]);
for(j in 1:M) {
s <- sum(x[[i]][[j]]);
if(isPrime(s)) {
print(c(s,x[[i]][[j]]));
}
}
}
}
a <- primes(1000)
b <- partitions(a)
printPrimeSumOfPrimes(b)
[…] If we take the 11 consecutive prime numbers from 157 to 211 & sum them up; we get 2011. Image via RepulicOfMath.WordPress.com […]
Leave a Reply
January 1, 2011 at 7:00 am
I don’t have Mathematica, and my R skills aren’t up to this, but I wonder something else ….
Are there an infinite number of prime numbers that are the sum of consecutive prime numbers?
January 1, 2011 at 10:36 am
Excellent question Peter. It looks like it from the growth of the primes that are sums of consecutive prime numbers, but right now I do not know a proof.
My R skills are definitely not (yet) up to writing code to do this in R, but it should not be too difficult, following the idea of the Mathematica code. I put summaries of two R packages to find partitions of integers, and to check if an integer is prime, at the bottom of the blog post.
January 3, 2011 at 7:35 pm
of course there are; a variant of Euclid’s proof of the infinity of primes will work, unless you have a prime number that doesn’t begin a chain of sequential primes that eventually sum to a prime. What’s the standard of proof?
January 4, 2011 at 8:34 am
Hi David – I don’t see how you would apply Euclid’s proof here.
Let’s call all the primes P and all the primes that are sums of consecutive primes S
1. Assume there is a largest S. Let’s call it X
2. Write down …. what did you have in mind here? All P smaller than X, or all S smaller than X?
3. Multiply them and add 1
4. Either the new number is a member of S or there is a member of S that is larger than X and smaller than the result in 3.
The first few number in S are 5, 17, 23. Let’s say we think 23 is the largest one. So, 5*17*23 + 1 = 1956. Not prime, obviously, but = 2*2*3*489, and 489 is not a member of S.
or, perhaps all P less than X?
2*3*5*7*11*13*17*19 + 1 = 9699691, which isn’t prime, but I don’t have a program that factors things quickly … perhaps someone else does.
In any case, I don’t understand how this proof would work
Peter
January 4, 2011 at 12:24 pm
the sense of that proof, that there are always more. You can start with any prime number and add consecutive primes to it until you get a prime. There are an infinity of primes, so an infinity of starting points, all resulting in a prime that is a sum of consecutive primes.
January 4, 2011 at 5:31 pm
9699691 is divisible by 347.
David has failed to prove his conjecture that “all prime numbers begin series of consecutive prime numbers which will sum to a prime” without presuming “there is no prime number that does not begin such a series” which is a restatement, therefore circular. How would one search for such a number? It’s nonexistence seems obvious, but obvious is often meaningless in math theory.
January 24, 2011 at 10:40 pm
Hi.
Euclid’s proof does not state a way of finding new primes. It just just produces a number that’s either a prime, or not.
If it is a prime, it adds to the “complete” list, and proves that there is no complete list of primes.
If it is not a prime, that means that there is missing a prime number amongst the list of the product: who can factor the new number/product….