When is an integer a square?

Posted by: Gary Ernest Davis on: November 30, 2010

In: Uncategorized
Comment!

0 Shares

This post came out of a conversation with James Tanton (@jamestanton) about squares of integers being exactly the integers not represented by rounding $n+\sqrt{n}$ for $n$ an integer (see here for background).

To say that rounding $n+\sqrt{n}$ yields an integer $k$ is to say that:

$k-\frac{1}{2} < n+\sqrt{n} < k+\frac{1}{2}$ ……………………………. (*)

Subtracting $n$ from the inequalities in (*) and squaring – as we can do and preserve the inequalities because the resulting left hand expression is positive – we get two quadratic inequalities for $n$ .

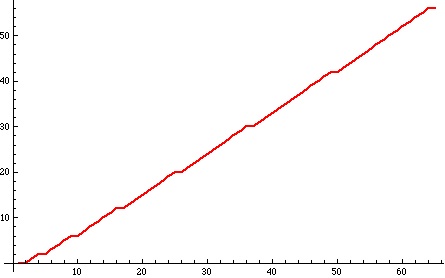
After some consideration of these inequalities I was lead to consider the function $F(k):=\textrm{Floor}[k-\sqrt{k-1/4}]$ .

Below is a plot of this function for $1 \leq k \leq 65$ :

What is striking is that there are little steps in the graph.

What’s more striking is that these steps occur precisely when $k$ is a square.

In other words this graph, and much more numerical evidence, suggest that an integer $k$ is a square exactly when $F(k)=F(k+1)$ .

I believe this, from the overwhelming numerical evidence, but I cannot yet see why.

Maybe someone else can?

Postscript

Nick Hobson (@quintic) provided a nice argument, in the comments below,Â that shows $k$ is a square exactly when $F(k)=F(k+1)$ .

3 Responses to "When is an integer a square?"

1 | Peter Flom
November 30, 2010 at 5:20 pm

I don’t have an answer, but I noted this:

(k – 1/4k)^.5 is either a whole number or a whole number + .5 when k is 3 12 27 48 75 ….

where the second differences are all 6.

Not sure what (if anything) this adds to the solution

Reply

2 | Nick
November 30, 2010 at 6:24 pm

Floor(k – âˆš(k – Â¼)) = Floor(k) – Floor(âˆš(k – Â¼)) – 1 = k – 1 – Floor(âˆš(k – Â¼)), for all k > 0, since âˆš(k – Â¼) is never an integer (because k – Â¼ is never the square of an integer.)

So F(k+1) – F(k) = 1 – (Floor(âˆš(k + Â¾)) – Floor(âˆš(k – Â¼))), which is clearly equal to 1 unless k is a perfect square, when it equals 0.

Reply

Gary Davis
November 30, 2010 at 6:51 pm

Thanks Nick. That’s great.

Reply

Leave a ReplyCancel reply