Why multiply binomials?

Posted by: Gary Ernest Davis on: January 5, 2010

In: Uncategorized
Comment!

0 Shares

This is a joint post of Gary Davis & Glenn Kenyon

Gary (left) & Glenn (right)

The issue

Glenn recently tweeted: Â Google Search on “Why multiply binomials” yields site on HOW, not WHY. Anyone out there know a reason why that 8th graders can relate to?

Searching the Web for a reason why anyone would be even vaguely interested in multiplying binomial expressions yields nada.

Reasons why are conspicuously absent (unless you count a vague reference that this might be useful somewhere in chemistry).

So is there a reason that might make sense to a grade 8 student, and their teacher, or is this another case of a technique that “will be useful in later mathematics” ?

Does knowing how to multiply binomials in any way empower, or enlighten – or even interest – a grade 8 student? Or is this just another boring exercise dreamed up by text book writers?

One possible answer to Glenn’s question is that Â multiplication of binomial expressions $ax+b \textrm{ and } cx+d$ , which represent straight line functions,Â is a way of constructing quadratic functions where we know in advance the location of the crossing points on the $x$ -axis.

For this answer to make sense, students need to be relatively comfortable with plots of straight line functions. If all they know is $ax+b$ as an expression involving the indeterminate letter $x$ then they are unlikely to see any meaning in multiplication of binomials, and will most often blindly manipulate them according to apparently arbitrary rules, the most notorious of which is encapsulated in the FOIL acronym.

Separating binomial expressions from straight line functions, and separating the multiplication of binomials Â from the construction of quadratic functions with specified intersections with the $x$ -axis is as silly as following the path of the Marginal Way, Ogunquit, with a paper bag over one’s head.

Relating multiplication of binomials to construction of quadratic functions raises the question, in turn, of why we might want to do that. What, in other words, is a problem that this technique solves?

The distributive law for numbers

The distributive law for numbers – the property that $a\times(b+c)=a\times b+a\times c$ for numbers $a,b,c$ is actually pretty useful.

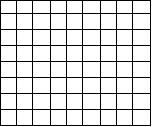
Here’s Â how a grade 3 kid used it once. Â This student was asked how many small squares there are in a rectangular grid of 8 rows and 9 columns:

The student must have thought this question was at least worth answering because he thought about it.Â Most kids like counting, and like to show what they can do. He answered “72”.

When asked how he got that answer he explained that if there were one more column, the number of squares would be $10 \times 8$ which he knew was 80. So he counted back from 80 to get a result of 72. In essence, this student knows that $9\times 8=(10-1)\times 8 = 10\times 8 - 1\times 8$ .

If you wanted to multiply 23 by 17 in your head one way to do it is to use the distributive law: $23\times 17 = (20+3)\times (10+7)$ $=20\times 10+20\times 7+3\times 10+3\times 7$ $= 200+140+30+21=391$ .

But, honestly, who these days is going to multiply big numbers in their head, especially examples like $1123\times 2124$ ?

A calculator has the distributive law built in, so a calculator can use the distributive law to do the tedious work for us. Apart from some small cute examples like $9\times 8$ or $23\times 17$ , Â or other cute examples set in text books to practice multiplication using a standard algorithm, what might be a reason for knowing and appreciating the distributive law for numbers?

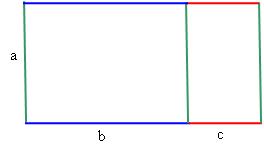
If we think of the positive numbers (whole numbers, fractions, decimals) as lengths, then the distributive law $a\times (b+c)=a\times b+a\times c$ is nothing more thanÂ the statement that the area of the large rectangle below is the sum of the areas of the two small rectangles:

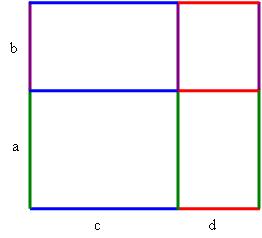
For positive numbers $a, b, c, d$ the extended distributive property $(a+b)\times (c+d)=a\times c+a\times d+b\times c+b\times d$ is the statement that the area of the large rectangle below is the sum of the areas of the four small rectangles:

The top two rectangles do not overlap the bottom two, so it is clear from the picture that this extended distributive property is just a double application of the simple distributive law.

This is the infamous – and purely instrumental – FOIL rule in a simple meaningful memorable picture!

But now we seem to be getting into algebra, so let’s look at the distributive law for algebraic expressions.

The distributive law for algebraic expressions

This can be tricky, depending on what you think of as an algebraic expression. Of course, a student knows the answer to that: anything with letters instead of numbers. So to a student, the distributive law $a\times(b+c)=a\times b+a\times c$ for numbers $a,b,c$ is already algebra.

Here’s where the muddle begins.

In one sense this is not algebra – it’s just a quantified statement about numbers. Â In another sense it’s the essence of algebra (depending on what you see as algebra.)

Students will often encounter the distributive law in the context of multiplying expressions such as $(2x+3)\times(x-1)$ . The distributive law is a key idea of algebra in middle school. Familiarity with the distributive law is appropriately gained Â in upper elementary school with the multiplication of two digit numbers: the distributive property can be mentioned very explicitly in this context.

Decomposing and recomposing of numbers is hugely important before entering into more generalized study in algebra. Â It is often a missing component in US education, according to TIMMS and other studies. The fact that distributive property can make more complex calculations easier, or allow people to program calculators to do arithmetic, tells us how central is the distributive property.

So now to Glenn’s question : why do we want to know, for example, that Â $(2x+3)\times(x-1) = 2x^2-2x+3x-3^2$ ?

How does his help us? What’s it good for, apart from passing high-stakes tests in order to get into and graduate from high school, or get into college?

It’s not hard to convince anyone that it is useful to be able to factor $2x^2-2x+3x-3^2$ as $(2x+3)\times(x-1)$ because the factorization will tell us where the quadratic Â function crosses the $x$ -axis.

So we might argue that in order to develop facility with factoring quadratics, it is helpful for students to develop a facility with multiplying out expressions such as $(ax+b)(cx+d)$ .

But now a thoughtful teacher has a dilemma. Multiplying binomials is not so intensely difficult as it is devoid of direct correlation to an $8^{th}$ grader’s understanding. It does seem like an important precursor to studying quadratics, but therein lies the dilemma: do all students studying Algebra I need to go through intensive study of how to work with quadratics in order to be deemed “successful” and “prepared” for the next level of mathematics? Even if they do, are they arriving to the next level of class able to take up where they left off? Is it lack of general meaning that is holding them back or lack of generalized practice.

Perhaps we can justify the multiplication of binomials as a way to gain sufficient fluency for the time they will be factoring trinomials. Sufficient practice with binomials ahead of time creates familiarity so that when they are factoring they can begin to predict what answers would and should look like.

Schematic hooks

We argue that lack of meaning and lack of practice are linked via the notion of schematic memory. Kids need a schematic hook on which to hang ideas like this, in order for them to be successful at mathematics.

What is a schematic hook? It is, in essence, a memory trace that allows a student to rebuild, or reconnect, a connected collection of relationships.

What is an example of a schematic hook? One example is the hook into the addition formulas for sin and cosine that comes from recalling that rotation through an angle A followed by rotation through angle B is rotation through an angle A+B. Then recalling, or refiguring, the $2\times 2$ matrix for rotation, and multiplying matrices, we get the addition formulas. So the simple schematic hook – vivid and memorable – is enough to allow us to reconstruct what it is we want.

Studies on memory in mathematical thinking in Russia in the 1960’s showed that this form of schematic hook is how capable mathematics students work: they do not rote memorize complicated formulas. Rather they develop schematic hooks that allow them to rapidly rebuild the formula. If they were to use a formula on a daily basis they would, of course, have quicker recall.

However – and this is an absolutely critical point – simply practicing procedures over and over will not generally result in longer-term memory, or in memory flexible enough to apply to new situations. Schematic hooks allow mathematics to be done more easily and with greater recall than without their use. The most likely reason for this is the relief to working memory afforded by schematic hooks. There is not as much to remember, and a schematic hook guides our thinking to a desired conclusion.

For example, when multiplying binomials Glenn relies on the image of a rectangle. This image comes from base ten blocks, coming from his years teaching array multiplication to $4^{th}$ and $5^{th}$ graders.

Schematic memory is very, very useful in our own learning, as students of mathematics and education. We both feel, however, Â that we have been less successful in convincing our own students of the advantages of establishing schematic hooks for concepts.

Students will grasp instrumental procedures, rather than establish schematic hooks, when they are frightened of being wrong. After all, if you have followed the stated rules, who can blame you if things go wrong? Establishing schematic hooks passes the authority for understanding to the student.

The danger, from the student’s point of view is that their teacher may grade them wrong if they use their own, yet powerful, ways of thinking. If the student just follows the teacher’s recipes then who can blame the student for getting it wrong? So, at least, seems to be their thinking.

Glenn has noticed that many students do not really accept algebra tiles: they donâ€™t see it as â€œrealâ€ algebra. He will spend up to 2 weeks on something, like multiplying binomials with tiles, with generic rectangles, but the students will opt for FOIL even if he has never mentioned or recognized it in class. This reliance on an instrumental recipe, over a schematic hook, is symptomatic of students who are nervous of being wrong.

Few of Glenn’s students really struggle with using FOIL, but give them a trinomial to multiply or cube a binomial, and they are all uniformly lost. And the reason is simple – an instrumental procedure applies only to that which it applies. Students cannot gain flexibility of thought – applying ideas and procedures in new settings – if they are thinking instrumentally, simply following a recipe. They necessarily have to learn to establish schematic hooks.

Cognitive roots

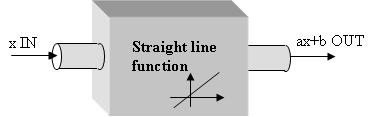
Closely associated with schematic hooks are cognitive roots. A cognitive root for a mathematical idea or procedure is a simplified schematic way of thinking about the idea that allows very easy entry for a beginner, is easily recalled Â often through heightened visual imagery, which may have to be elaborated on as a student develops deeper understanding, yet which is never discarded. A classic example of a cognitive root is that of the function machine model of a function, with an input and an output:

This diagrammatic interpretation of a function is readily brought to mind, encapsulates the essential aspects of a function of a single variable, and while students may develop more sophisticated notions of functions they do not need to discard the function machine model.

The FOIL recipe by itself is not a cognitive root. The reason is that it is a recipe without a reason – a procedure without a why or wherefore. If – and this is a very big if – FOIL were linked to the area diagrams above, Â it is possible it might become a schematic hook for some students. In other words, if students recalled the diagram as they multiplied binomials, and saw why the multiplication works as it does, then they might have a schematic hook.

Multiplying straight line functions

Below is one perspective on a cognitive root for quadratic functions that may allow a student to develop a schematic hook for multiplying binomial expressions. First, it is important, in this scheme, that students know about straight line functions:

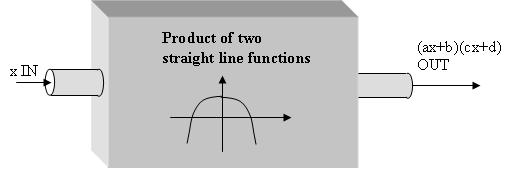
Then, multiplication of two straight line functions comes about by running the output from two straight line function machines through a multiplication function machine:

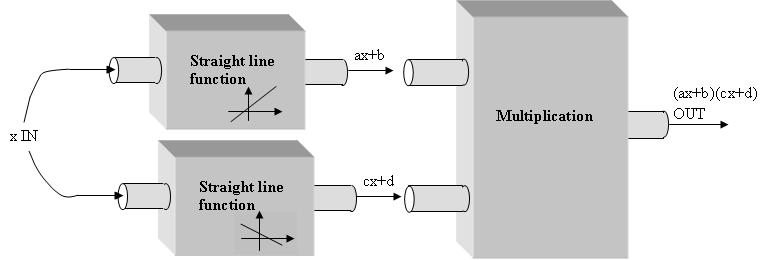
For most students, and perhaps some teachers, thinking of multiplication as a function of two variables is already novel.

This entire function machine apparatus can be represented in terms of input $x$ and output $(ax+b)(cx+d)$ as follows:

From this perspective we can see how relatively complicated – for an $8^{th}$ grader -Â is the idea of a product of two straight line functions. And now we see how this is all swept under the rug by getting students to mindlessly use FOIL on expressions such as $(ax+b)(cx+d)$ rather than thinking about these expressions as shorthand for straight line functions.

Emphasizing functional relationships

What is important in this approach is that we think of an expression such as $ax+b$ as shorthand for a function, the function that assigns to a number $x$ the number $ax+b$ .

If middle and high school teachers want to go down the route of treating expressions such as $ax+b$ as abstract expressions, divorced from an interpretation as functions, then they are treading dangerous water, involving themselves and their students in deeper abstractions than they probably realize.

The function scheme seems to be a sensible schematic hook on which to hang multiplication of binomial expressions $ax+b \textrm{ and } cx+d$ : it is a way of constructing quadratic functions where we know in advance the location of the crossing points on the $x$ -axis.

Further, it relates to the observation that adding two straight line functions still gives a straight line function, but multiplying two straight line functions produces a a curved function – a quadratic.

Difficulties that students have in seeing $2x$ , for example, as a term can be tackled, in this approach, by seeking a function $(ax+b)(cx+d)$ where $a, b, c, d$ are whole numbers, that crosses the $x$ -axis at $\frac{1}{2}$ .

Cognitive theft

By over-emphasizing an instrumental procedure such as FOIL, to the exclusion of Â relational thinking about why the answer would be as it is, teachers are stealing from students the possibility of sensible human engagement with this topic.

This is an example of cognitive theft, in which an instructor substitutes an instrumental procedure – a cheap recipe shortcut – for a deeper understanding of the topic and its relationship to other aspects of mathematics.

By allowing students to only use FOIL, we are Â robbing them of some visual and logical explanation of what is going on. By insisting they work with other models we irritate them to some extent, but also guarantee them some extra input as they develop their own schematic memory.

We work with the assumption that each individual makes their own meaning of anything they learn: in other words, they create their own schematic memory and cognitive roots. One of our tasks as teachers is to ensure they have a wide variety of Â sources available to them in this endeavor.

Why do we want to construct quadratic functions with prescribed roots?

An obvious question related to meaning is: why do we want to construct quadratic functions with prescribed roots anyway?

Of course we can ask this question of any topic in mathematics, and not all students need applications to make mathematical questions meaningful. In fact, it is a certain narrowness of vision in mathematics education to make the entire curriculum immediately useful and available to the learner at their developmental level. There is power and relevance in learning mathematics as an abstract and pattern driven activity, and as an amazing cultural artifact of human development.

It seems to us that there is, in fact, no compelling reason to learn to construct quadratics with specified roots other than the intrinsic interest of so doing. That is not a crime. It is not a valid reason not to learn how to do multiply binomials to do it. The main reason we learn to multiply binomials is to prepare ourselves for the useful task of plotting quadratic functions vis-a-vis the x intercepts. In turn, we can then construct a series of situational problems that while perhaps challenging to relate to the adolescent mindset, at least can provide a â€œreal worldâ€ setting to justify their use. This is like shooting hoops in basketball practice: getting ready for a real game requires practicing a skill in more restricted set-ups

Moral ?

If there is a moral to be learned from the difficulties kids have with multiplying binomial expressions it is this: mathematics is a highly interconnected subject; separating one small topic and treating it in isolation, with only instrumental procedures, is highly likely to leave students with a sense of alienation and lack of meaning for what they are doing.

This is a way to produce mindless robots, not intelligent young people.