Nigel Smith was a teacher at Twyford Preparatory School, Winchester, England. He was my friend and colleague. He died of brain cancer at age 44, 8 years ago. I still miss him deeply and I want to write about some things we did together in his class at Twyford.

Twyford School, Winchester

I met Nigel when he enrolled as a graduate student in education at the University of Southampton, where I was Professor of Education.  Nigel and I hung out quite a lot. We drank together, at home and at local pubs, and had long conversations about mathematics teaching. Many of these were with another colleague, David Hill, who taught mathematics at Hordle-Wallhampton School near Lymington where Nigel was previously Head of Mathematics.  The three of us would go to David’s house and then walk a few hundred yards to his local pub, the Chequers Inn, for lunch. We ate, drank, walked and talked. We wrote articles together, and enjoyed each others company.

Nigel taught grades 5 through 8 at  Twyford, which is a “prep” school. What this means is that children at Twyford were being prepared, or “prepped”, to enter the competitive private schools – known as public schools in England – such as Eton, Rugby and Winchester. Parents pay large sums of money to send their children to prep schools, and teachers are expected to obtain good results. This means, in practice, success in getting students into the major public schools. Nigel was good at his job, and his students regularly scored very well on admission tests. His continuing employment depended on his ability to get his students through these admissions tests.

Yet Nigel did not simply “prep” his students in test-taking. In fact he did this relatively rarely. What he did do, a lot, was to make mathematics interesting, fun and exciting for his students. He did this by experimenting with investigations, some of which we worked out together.

Nigel’s Head-teacher – his Principal to U.S. readers –  asked the IT teacher who at Twyford was most innovative in the use of technology in their teaching. The IT teachers’ response was: Nigel Smith. Yet Nigel could barely make his way around Microsoft Word, so how did he get this – well-deserved – reputation?

Nigel used technology because it furthered his aim of creating an open, questioning approach to learning mathematics.

I recall several examples of the use of technology to further his aims of  mathematical investigations. These, as I recall, were  used with grades 7 and 8:

(1) Data analysis using Excel

Nigel had devised an investigation, the details of which escape me, involving a tortoise and hare race. Students did calculations – by hand – and plotted the resulting data in Excel, looking for straight line and quadratic fits to the data.

(2) Conway’s Game of Life

I introduced Nigel to Conway’s Game of Life and he was bowled over by it.  He thought it an excellent vehicle for investigation and reasoning. Nigel gave the students a few starting points and then let them play for the first lesson. He set as homework the problem to explain why gliders glide. Anyone can see that they glide. Nigel’s question was: why?

Nigel’s students worked at creating complex eventually-periodic cellular automata, some of them with periods on the order of several hundred.

I was in Nigel’s class one day when the Head-teacher brought parents of a prospective student into the room to show them features of the mathematics program. The Head teacher and parents approached me and asked what the boy next to me was doing. I said: ” Why don’t you ask him?”  This boy then explained in a most articulate way, how they were investigating repeating cellular automata, of which the glider was a simple example. The Head-teacher and visitors left very impressed.

(3) Secret codes

Nigel and I discussed a lesson sequence based around simple ciphers. Our aim was to introduce the students to the use of modular arithmetic in a practical setting of devising and cracking secret codes, beginning with simple substitution codes.  The students loved this activity. They worked in small teams, competing one against the other, encoding and trying to crack the coded messages. They used Excel to carry out modular arithmetic, and code their message.

At Christmas break we gave the teams an exercise to set a reasonably long coded message for other teams to try to crack over the break. I explained to the students that most coded messages were not cracked by intelligent application of decoding  skills, but rather by breach of protocol or by coercion. A student asked what that meant. I explained breach of protocol as not following the set procedure for coding, using Alan Turing and others’ cracking of a German code as a result of a breach of protocol.  I explained coercion through the example of torturing someone who you knew held the key to the code. At that point, one team became very excited and asked Nigel if they could torture the other teams!

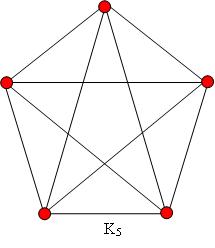
(4) Non-planar graphs

Nigel had students draw graphs on paper and discussed the concept of plane and planar graphs. As I recall he used a graph drawing program (it may have been Cabri Graph) that allowed topological reformation of graphs. A main topic of investigation was whether the complete graph on 5 vertices was planar, and if not, why not.

After much drawing, discussion and argumentation, the students came to he conclusion that   is not planar. Their arguments used the Jordan curve theorem implicitly. That is, they did not know, or articulate, the Jordan curve theorem, but from our perspective acted as if it were true.

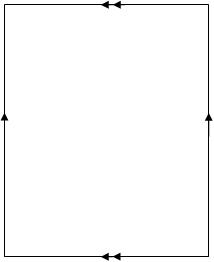
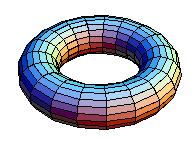
The next lesson Nigel and I got students making graphs on a torus, with the aim of them seeing that  can be drawn on a torus  so that edges meet only at the vertices. We gave them a choice of 3 models of a torus:

(a) A polystyrene solid torus, bought at a local  craft store. Vertices were stick pins, and edges were long pipe cleaners.

(b)  A sheet of paper on which they could draw edges of the graph, with the usual edge identifications to make a torus:

(c) A computer-generated image of a torus in a Microsoft Word  document, on which they could draw vertices and edges, using a drawing program:

About half the class used physical models, a few students used the paper sheet with identifications, and the rest – almost half the class – used the computer image.

It turned out that a student whom Nigel, to that point, regarded as  one of the least mathematically able in the class, was the first to show that is a torus graph. He used the physical model.

So how did Nigel, who was not even Microsoft Word savvy, use technology in such a productive way to further his aims in creative mathematical exploration? Answer: he asked others for help, including students. If a student knew how to use Excel or Word to do something that Nigel did not, he would ask that student to explain to the rest of the class. Nigel never stood on ceremony. He was a partner in his students’ learning. He learned with them.

He was a wonderful teacher, a close friend, and I miss him so much that it hurts to write this.  Ave atque vale, Nigel.