The value of cos(pi/5)
Posted by: Gary Ernest Davis on: December 3, 2010
@capedsam Tweeted: “Can you find an exact value for cos(pi/5)? “

x
It is actually fairly easy to find an exact value for  by following a path through the complex numbers.
by following a path through the complex numbers.
x
To do this we use Euler’s identity  for all real numbers
for all real numbers  .
.
x
Jim Tanton (@jamestanton) has a very nice introduction to Euler’s identity here.
x
As shorthand let’s write 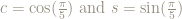 .
.
x
From Euler’s identity we know that:
x
x
We raise both sides of equation (1) to the 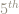 power:
power:
x
x
The left hand side of equation (2) is  .
.
x
The right hand side of equation (2) is, by the binomial theorem:
x
x
We separate the expression in (3) into real and imaginary parts, and equate the real part to -1, and the imaginary part to 0:
x
x
x
We can substitute 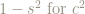 in (5) to get:
in (5) to get:
x
x
Expanding (6) and dividing through by  we get:
we get:
x
x
This is a quadratic equation for  with roots
with roots 
x
This gives 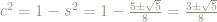
x
Only one of these two roots can be equal to 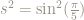 .
.
x
Which one?
x
We know  so
so  .
.
x
Therefore, 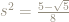 so
so  which means, since
which means, since  , that:
, that:
x
x
One can also get the quadratic equation for  from the multiple angle formulas (if one can remember them!).
from the multiple angle formulas (if one can remember them!).
4 Responses to "The value of cos(pi/5)"
Here’s another: write sin 3pi/5 = sin 2pi/5, expand into sines and cosines of pi/5, and divide out the sin pi/5 which should show up in every term. You’re left with a quadratic in cos pi/5.

December 3, 2010 at 11:17 am
Note also that cos(pi/5) = (1+sqrt(5))/4, which is half the golden ratio. Can you find a geometric proof?
December 3, 2010 at 11:21 am
Nice question. Thanks.
Of course
January 14, 2011 at 12:29 am
1). Connect all of the vertices of a regular pentagon.
2). Use similar triangle ratios to show that the sides of the 36-72-72 isosceles triangle are related by the golden ratio.
3). Use law of cosines to prove that cos(36) = phi/2