Imagine you get to choose one of each type of cake from the cake shop pictured above!

What a treat!

With trembling hands you go from one type of cake to another, carefully choosing one of each until you’ve run out of different types of cakes.

Yum!

When you’re done you have a collection of cakes, with one cake from each type of cake.

Infinitely many choices

This is such a natural procedure that mathematicians imagined, without really thinking about it, that the same type of choice could be carried out even if there were infinitely many different types of cakes to choose from.

Ernst Zermelo (1871 - 1953)

Until Ernst Zermelo made it clear that it was a foundational axiom, or assumption, of set theory that one could always make such a choice.

Where in mathematics might one need to make a choice from one of infinitely many different types of collections?

Here is one simple example:

The Cartesian plane consists of ordered pairs of real numbers .

We can shift points in the Cartesian plane by moving them left or right one unit, or up and down one unit.

The orbit of a point in the Cartesian plane for this group of motions is the collection of all points that can be moved to by moving it up, down, left or right one unit, repeatedly.

In other words the orbit of consists exactly of the points where range over all possible integers.

The orbits of points split the Cartesian plane into disjoint sets.

Is there some way of forming a set that consists of just one point from each possible orbit?

We can answer this positively by first observing that the orbit of each point on the Cartesian plane passes through the square with corners exactly once, except for points on the lines joining to and to , and the lines joining to and to : for any point on these lines, its orbit passes through the square exactly twice (once on each edge).

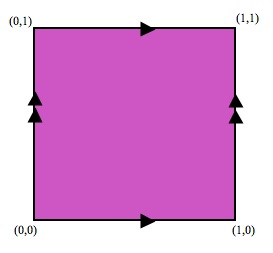So, if we identify (= glue together) the edges of the square as indicated, we will  have a set of points that (is in one-to-one correspondence with a set that) contains a single point from each and every orbit.

This identification gives us a torus:

So the answer to our question is: “Yes. we can find a set (the torus) consisting of one and only one point from each orbit.”

If we fancifully imagine the orbits as types of cakes, and points in each orbit as cakes, then we have found a set that consists of one and only one of each of the infinite types of cake.

Axioms of choice

Zermelo’s phrasing of the axiom of choice was as follows:

“If T is a set whose elements all are sets that are different from ∅ and mutually disjoint, its union ∪T includes at least one subset S₁ having one and only one element in common with each element of T“.

Ideas about infinity, and infinite processes, are essential to mathematics, so Zermelo’s axiom of choice came to play a central role in the foundations of mathematical thought.

Independence of the axiom of choice

Kurt Gödel

Paul Cohen

Kurt Godel and Paul Cohen showed that the axiom of choice is independent of the other axioms of Zermelo-Fraenkel (ZF) set theory. Assuming ZF set theory is consistent, Godel constructed a model of set theory in which the the axiom of choice cannot be disproved from the other axioms. Cohen constructed  a model of ZF  set theory in which the axiom of choice cannot be proved from the other axioms.

Godel and Cohen’s theorems together tell us that we can take the axiom of choice as an axiom, or take its negation as an axiom – it’s up to us to decide in which set-theoretic world we want to live.

Now that IS choice!

Nice things with the axiom of choice

1. We say that a set is larger than a set if there is a one-to-one function . (“One-to-one” means if )

The axiom of choice allows us to conclude (indeed, is equivalent with): for any two sets either is larger than or is larger than .

2. A set is countably infinite if it can be put into one-to-one correspondence with the set of natural numbers.

The axiom of choice allows us to conclude that a countably infinite union of countably infinite sets is again countably infinite.

Weird things with the axiom of choice

1. The axiom of choice allows us to prove the Banach-Tarski theorem:

A ball of radius 1 in 3-dimensional real space can be dissected into a finite number of pieces which can be re-arranged by rotations and translations to yield two balls of radius 1.

As you might suspect, these pieces do not have a rotation and translation invariant volume.

I was prompted to write this post by someone saying they were puzzled about the reference to the axiom of choice in the following XKCD cartoon:

Courtsey XKCD

2. A total order on a set is a relation between pairs of elements of (a binary relation), denoted , with the following properties:

A first element for a subset for a total order is a such that .

The axiom of choice allows us to conclude that there is a total order (not the usual order !) on the set of real numbers such that every non-empty set of real numbers has a first element.

Indeed there is nothing special about the set of real numbers in this respect: we can replace it by any set whatsoever.

Nice things without the axiom of choice

No Banach-Tarski paradox.

Weird things without the axiom of choice

There is a model for ZF set theory with the negation of the axiom of choice in which the set of real numbers is a countable union of countable subsets (but, of course, is not itself countable).

Last words

To paraphrase Horst Herrlich:

Mathematics with “choice” may be as unreal as a soap-bubble dream, but mathematics without “choice” is as horrible as nightmare.

We might also say that you have to know if you can choose your cake before you can eat it.

And we couldn’t pass up the old, but golden, riddle: “What’s yellow and equivalent to the axiom of choice?”