Is rationalizing rational?
Posted by: Gary Ernest Davis on: May 3, 2011
Rationalize or get it wrong?
Text books and test setters regularly mark students wrong if they give an answer of to a problem.
A student is supposed to know, as part of mathematical convention, that should be rationalized to
.
This issue has been discussed before by @suburbanlion at SuburbanLion’s Blog and @jamestanton at Rationalising the Denominator, among others.
Marking a student wrong for not carrying out a rationalization like this is just BS (and I don’t mean “Bachelor of Science”).
And there is no such mathematical convention – it’s made up by people who write text books and set tests.
This issue came up again recently in #mathchat when @davidwees wrote: “I tell my students that people used to rationalize denominators b/c it made calculations easier” and “1.414…/2 is much easier to do than 1/1.414… without a calculator.”
My issue with what David wrote (and indeed with part of what James Tanton says in his video) is how, without a calculator, do we know that ?
Of course if someone told us that and we figured that
then we could probably be adept enough to calculate
by hand.
The field ![\mathbb{Q}[\sqrt{2}]](http://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=8E8778&s=0&c=20201002)
Numbers of the form where
are rational numbers (fractions) collectively have a remarkable structural property:
not only can we add, subtract and multiply such numbers and still get numbers of the same form (e.g. ), we can also divide such numbers and still get a number of the same form:
e.g.
Collectively, numbers of the form constitute a mathematical field, denoted by
– a structure in which addition, subtraction, multiplication and division (by non-zero numbers) is always possible.
From this perspective, rationalizing is just expressing the fact that the reciprocal of
is again in the field
.
What about rational approximations?
There are technical senses in which the continued fraction of a real number gives the “best” rational approximation to that number.
So how do we find the continued fraction for ?
We are looking for an (infinite) expression of the form :
where the are whole numbers.
Because the piece after
is less than 1, we see that
is the largest integer less than
, which is 1 (we know
because
).
This leaves so taking reciprocals we see that
.
This means that is the largest integer less than
.
In other words, , which means that
.
We know because
, so
.
Continuing in this vein gets trickier, because next we have to find the largest integer less than .
Because satisfies a quadratic equation we can use a cute trick to find the continued fraction for
.
Let’s write so that
.
Dividing by gives:
Taking this to a limit we get .
Since we get
.
By successively terminating this continued fraction we get the following rational approximations to .
This immediately gives us the following rational approximations to .
Newton and the Babylonians
Isaac Newton’s method for finding roots of functions, applied to the polynomial leads directly to a method for approximating
known to the Babylonians.
Using this method we start with an approximation – let’s start with
because its the first approximation from the continued fraction for
: it’s the integer part of
.
We then average to get the next approximation
.
We generate a sequence of rational number approximations to
where. at each step,
.
This gives us the following rational number approximations to .
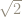 as a decimal
as a decimal
So now we know how to approximate by rational numbers, we can use the rationalization
to get rational approximations to
, but you see the absurdity – why bother? Just invert the rational approximations to
.
How about the decimal expansion of – where does that come from?
Decimal approximations to are usually obtained from the rational approximation from the continued fraction, of from the more rapidly convergent Newton’s (= Babylonian) method.
The record at the time of writing this post is is 1,000,000,000,000 decimal places due to S. Kondo & A.J. Yee in 2010.
The empirical evidence is that is normal in base 10, meaning that, to date, each of the digits appears with proprtion
, each pair of digits with proportion
, each triple of digits with proportion
and so on.
However no one yet has a proof of this.
8 Responses to "Is rationalizing rational?"
I think I was making the assumption that in typical calculations, one has a table in which they can look up an approximation to the square root of 2 to whatever accuracy has been previously calculated, and then use that approximation in their further calculations. Is it not true that engineers would have relied on tables of values in their calculations and that rationalizing the denominator of a fraction would have made those calculations easier for them to do?
Interesting post. I’d always get frustrated at school when the teacher couldn’t say why giving the final answers in rationalized form was so important. Now I have a wider view of things.
I have a question about your division example for numbers in Q[sqrt(2)]. Surely the numerator in the middle step should be 8 + 5(sqrt(2))? Which makes the rest of it incorrect? If I’m wrong, please excuse me, and if I’m right, please excuse my pedantry.
I want to marry you.
Okay, wait. Maybe that’s not the best comment to make on a blog. Do-over.
Thanks so much for this, Gary. I’ve been a non-rationalizer for years. So much so that I’ve informed students of my willingness to beat up any subsequent math instructor they have that makes them rationalize. Nobody’s taken me up on it. (bummer)
This reminds me of the Pythagorean’s murder of Hippasos for proving root 2 as irrational. I love math-based cults!
I have gone back and forth on this – but usually come back to teaching students to rationalize denominators mainly because they will run into it so often “in future math classes”. When asked why it is necessary, I show them since an irrational number has an infinitely long decimal representation, dividing 1 (or any rational) by that irrational number is “impossible”. (First make the dividend a whole number by moving the decimal point an infinite number of places, then …).
It has really become a requirement for all mathematics students in West African Examinations to write answers in fractions sucth that the divisor must be greater than the dividend.


May 3, 2011 at 11:34 am
Nice derivation using the fact that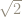 satisfies a quadratic, and I like the rational approximations both to
satisfies a quadratic, and I like the rational approximations both to 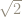 and
and 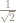 .
.
I’m not a rationalizer either, preferring to write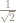 primarily because it looks more like what it is: namely, the square root of
primarily because it looks more like what it is: namely, the square root of 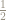 .
.
I always assumed that rationalizing had something to do with the monks of yore having tables of square roots at hand; if you can look up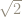 , it’s easier to divide that approximation by 2 than 1 by that approximation. (I guess monks = medieval calculators). Either way, not a sensible reason nowadays.
, it’s easier to divide that approximation by 2 than 1 by that approximation. (I guess monks = medieval calculators). Either way, not a sensible reason nowadays.