In the video below, Aziz Belhassane Sensei is demonstrating Aikido at the Sugano Shihan Memorial Summer School 2011.

Whether you know Aikido or not, the thing you will notice, especially if I point it out to you, is that Aikido is not a spectator activity. You cannot learn Aikido simply by watching someone else. Watching is critical, paying attention is critical, but doing is the essence.

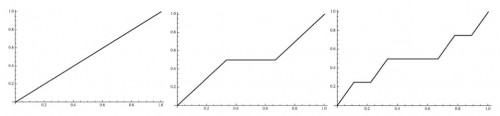
Currently I am teaching a small class – 11 students – what is known in the U.S. as Advanced Calculus. This is their second semester of Advanced Calculus, and I am conceiving it as an introduction to real analysis. This past week we have been looking at the Cantor function (also known as the Devil’s Staircase).

The Cantor function can be described as the limit of a sequence of piecewise linear functions. The first 3 are shown below:

The piecewise linear functions can be defined on the interval recursively as follows:

So we have a potential pictorial and recursive understanding of the sequence of approximations to the Cantor function.

These do not make it immediately obvious how to calculate the value of the Cantor function at a given point in the interval , particularly at points of the Cantor set, such as .

A simple recipe remedies this:

Write base 3 (with no all 2’s from some point on ). If one of the replace all digits after the first such occurrence by 0. Then convert all occurrences of 2 to 1 and read the new number base 2.

For example, base 3, so, according to the above recipe,  the value of the Cantor function at is base 2, which is .

The issue for the students was to reconcile the pictorial and recursive approximations to the Cantor function with this recipe.

Sadly, as was the case for most of the semester, they sat in silence waiting  for me to do something, even though the course is seminar style in which they present their efforts at problem solving. So I gave them all marker pens, got them up to the board, and got them working and talking. Eventually most of them started thinking.

In my view, mathematics is best done on your feet, actively moving.

What do you think?