How many zeros are there in 2^n?
Posted by: Gary Ernest Davis on: April 23, 2011
An old problem asks if is the highest power of
whose base
representation:
, does not contain the digit
.
For instance, the next powers of
do indeed contain the digit
:
x
How many zeros?
Instead of asking the existential question “Is there a zero in the base representation of
for
?” we can ask the more quantitative question: “How many zeros are there in the base
representation of
.
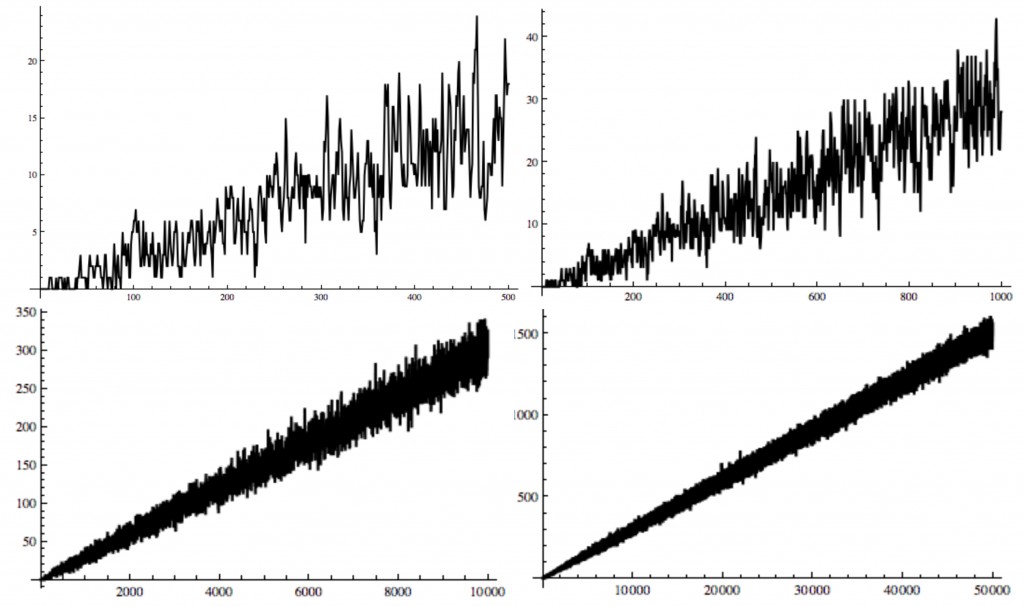
Here are plots of the number of zeros in the base representation of
for
up to
respectively:
We see, progressively, what seems to be oscillations around a straight line.
What could this straight line be?
And how large are the oscillations?
A straight line model
The number of digits of isÂ
, where
is the integer part of
.
Neither the first nor last digit of is
, so there are
digits of
that can be
.
If we assume that all digits
are equally distributed among these
places then we expect to see about
zeros in base
representation of
for large enough
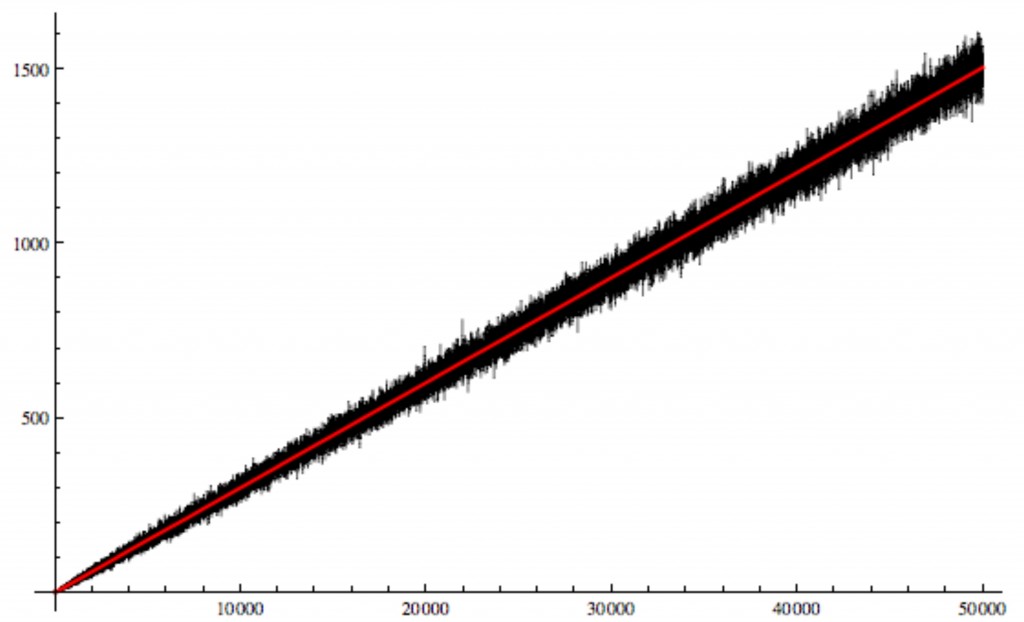
So we take as a linear model for the number of zeros in base representation of
the quantity
To get a visual feel for how this fits let’s plot the actual number of zeros along with this linear model:
The nature of the “error”
We now have a statistical model for the number of zeros, in the base
representation of
:
where we will refer to as the “error” (meaning how much
differs from the linear model).
How does the error behave?
In particular, how is it distributed?
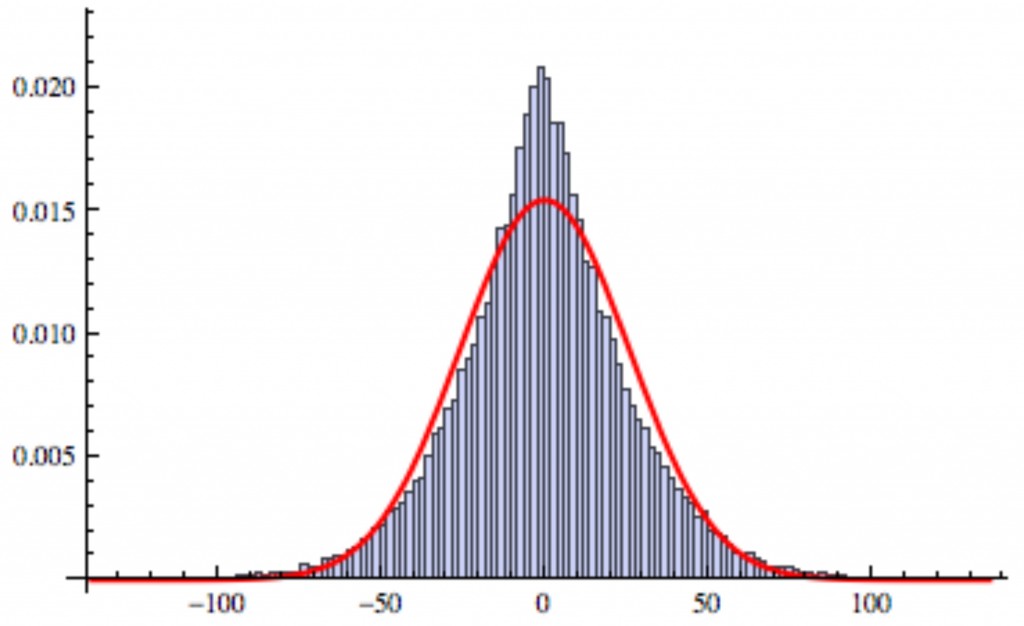
Below is a histogram of the error for
, together with a normal curve of the same mean and standard deviation:
We can see the the empirical distribution of the error is “peakier” than the normal distribution, and this is borne out by the kurtosis which is , substantially greater than a kurtosis of
for the normal distribution.
Plotting these histograms for various values of indicates that the variance of the distribution of the errors
varies linearly with
, or, what amounts to the same thing, the standard deviation varies with
.
Bounding the error
What we really seek is a bound on the errors sufficient to show that for large enough
.
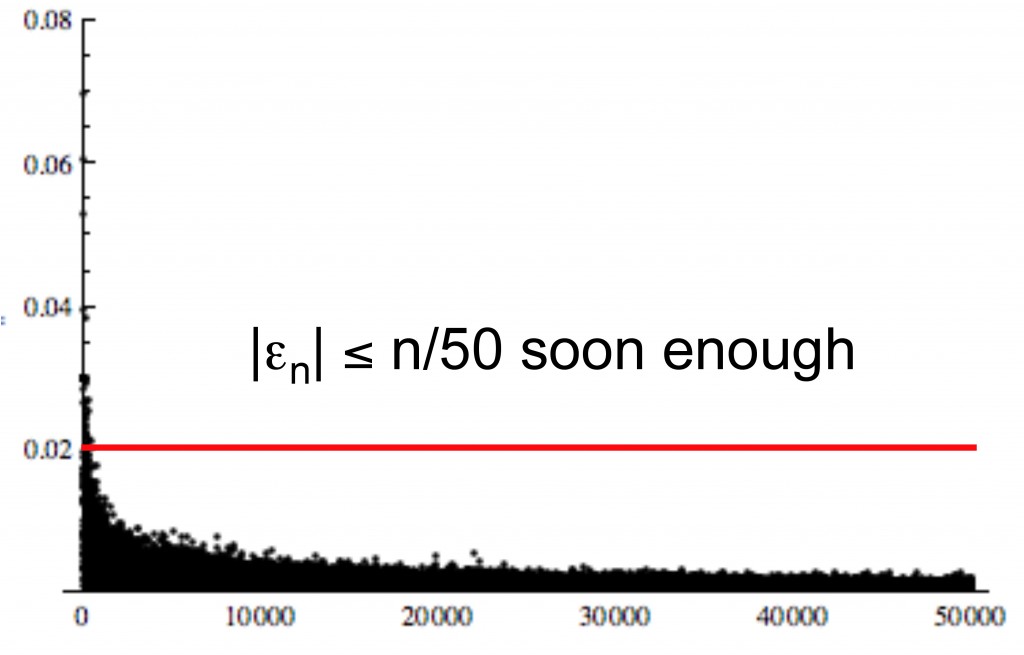
What does computation suggest?
Below is a plot of the size of the error divided by
.
It appears that even for quite small
:
If this does hold good then
So now we have a more precise statement: prove that for
.
Maybe techniques of higher order Fourier analysis (Higher-Order_Fourier_Tao) could be brought to bear on this problem since they are useful in proving other equidistribution theorems? Then again, just because Weyl’s polynomial equidistribution theorem can be interpreted as a higher-order Fourier analysis application may have nothing at all to do with equidistribution of digits in .
6 Responses to "How many zeros are there in 2^n?"
2^22 ends in …04.
@Xan: “The tens digit can also never by 0.”
2^23 = 8,388,608
Did I misinterpret what you said?
You wrote Epsilon/n <= 50 above your final figure. I think you meant to write Epsilon/n <= 1/50. Otherwise, it was an interesting read.

April 24, 2011 at 1:28 pm
The tens digit can also never by 0. (You can reason it out or just look at the 2^n mod 100 cycle.) I don’t think it affects the slope of your model, but it would affect the intercept. Maybe that would make your histogram be better centered on the normal curve.