Sandra was a pre-service elementary teacher at Rutgers in New Jersey. She came to mathematics methods classes with relatively low expectations:

“When I enrolled in this class back in September, I thought I was signing up for a three-month crash course in the mechanics of mathematics -something which had always eluded me. At that time I could not imagine math as anything more than the relentless stream of equations I used to agonize over as a young student.”

As the weeks went by Sandra’s written reflections reveal that she soon came to class with a specific intention of gaining enlightenment. She was not a student who simply attended class in order to have her presence recorded. She came with specific intentions, one of which was an expectation of moments of insight:

“Last week’s class was wonderful. For the first time since we began, I experienced the succession of ‘ah ha!’ moments I had been waiting for so eagerly.”

As instructor, I was unhappy that students were not expressing clear and unambiguous connections between the combinatorial problems that I had given to them to work on.

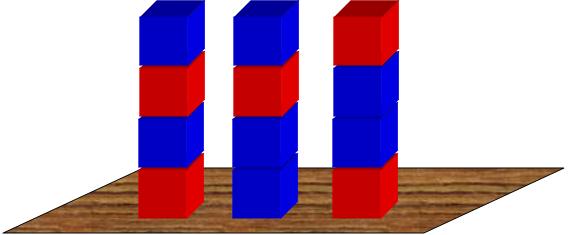
One problem was to figure the number of different block towers  of a given height that can be built from a large supply of red and blue blocks:

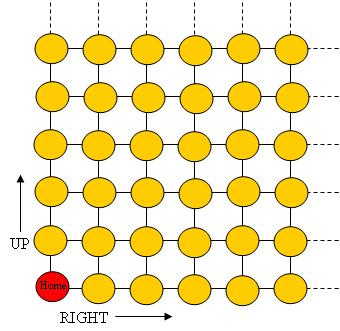
I took another of the combinatorial problems and added an element of chance to it. Students were to toss a coin 4 times in a row.  Starting from the HOME spot on the grid, below, they would, at each toss of the coin, move one step UP on the grid  if the coin came up heads, and RIGHT if the coin came up tails:

The question I set the students was: how will the number of times you land on a given dot pan out as you toss the 4 coins many times?

My aim was to stimulate students to build explicit connections between moves on the grid, and block towers.

Initially Sanda had not seen a connection between the two problems that satisfied her:

“We had been encouraged to think of the two colors in the towers as similar to the ‘Up’ vs. ‘Right’ options in the dot matrix, but this was difficult for me. In the ‘Towers’ activity, we used powers of two and increased them based on the number of blocks in the towers. But with the matrix (= grid), we plotted the number of options to each dot …I did not see powers of two in any of the numbers I was writing in the dots.”

However, with the coin-tossing procedure she suddenly saw something much different:

” As we did the activity, tossing a quarter four times each, I saw that there were only a limited number of answers for each toss based on the constraints of the problem…only 2 sides to the quarter and only four tosses. And I quickly saw that those dots were beginning to arrange themselves along a diagonal. And what did all those dots along that diagonal have in common? They were the only solution you could have when tossing a quarter exactly four times. And if you added up the number of options along that diagonal, you got a number which was 2, 4, 8, 16, 32 & 64 respectively. Powers of two. Suddenly I saw why the ‘Towers Problem’ could be solved using powers of two … and I saw how increasing the blocks in the towers moved the answers to the next diagonal and thereby to the next power of two. And I saw how the number of options increased systematically as each square’s options compounded with the addition of more variables.”

Sandra understood – she saw – that the rows of Pascal’s triangle – the diaognals of the grid -  add to powers of two. However, Sandra’s deepening perception and understanding of connections did not stop there. With the sudden understanding for how the powers of two entered the picture she made another fundamental realization about the proportions of marks on the grid spots 4 steps from “home”:

“Now I could see fractions expressed in our grid, because each dot represented a specific fraction of chances that it could be expressed given the intervals.”

This realization was both emotional and liberating. In one short episode of about 20 minutes Sandra woke from her mathematical slumbers:

“And I knew then, that different approaches worked for different people, and that’s why we need to acknowledge all the different ways we solve a problem. For some people building towers worked, for some it was the grid matrix and for others it was (a+b). it was tremendous to feel something abstract becoming concrete…to finally see algebra as a way of making sense of the world around you. I saw the connection between the 4 toss quarter game and the dot grid. I saw the way the number of tosses translated into a diagonal line across the grid. And I saw how certain dots were ‘hit’ more than others due to the number ways (sic) to reach that dot. And what was most momentous to me was seeing that the number of dots or ‘hits’ along that diagonal added up to a number that equaled the power of two associated with the number of ‘intervals’ or ‘jumps’.”

That moment of seeing a connection – of the mind and brain constructing a new vision of the perceptual material already in front of the student – is powerfully emotional:

“SO what have I learned? Well, that sometimes, it takes a number of different approaches or methods to help students understand math. It didn’t become clear to me until we did the coin toss. And there was a rush of connections and insights.”

Toward the end of a fifteen week semester – some 9 weeks after she had a sudden insight into connections between towers, grid walks and binomial expansions, and coin tossing – Sandra worked in a group on determining empirically the distribution of black and white sides showing when 6 Othello pieces (black on one side, white on the other) were tossed randomly from a bag.

Sandra, unlike others in her group, detached from the empirical activity and began drawing a grid, labeling the spots on the grid with the number of different ways of reaching that spot by walking UP or RIGHT (the entries in Pascal’s triangle). She worked at this until she completed the 6th diagonal.

When the class results for the empirical activity were pooled the result was 3 whites and 3 blacks occurring most often – 29 % of the time.

Noting Sandra’s approach, I asked her what she had obtained. She replied with an answer of 20 divided by , which another student calculated as 0.31.

This was a stunning example of flexible thinking, using long-term knowledge in a new context. Yet Sandra was critical of her memory in a reflection written after this episode. She apologized, following the class, for not being able to remember the entries in the  6th row of Pascal’s triangle, and described her memory as “poor”.

Sandra’s “rush of connections and insights” were emotionally laden cognitive insights that etched themselves deep in her memory. They impressed themselves so powerfully in her memory that she was able, during the remainder of the semester to bring these memories back to mind and to use them in differing settings, some not directly related to the context in which the memories were formed. However Sandra’s recollections of those memories was, in her view, “poor”. She still equated good mathematical memory with rote recollection of complicated formulas or facts, in precise detail, rather than a recollection of a broad cognitive road-map, based on an emotional episode.

Sandra also wrote in her weekly reflections:

“I look forward to those rare, but beautiful opportunities to make connections across the discipline, knowing that it is those eureka moments which make it all worth while. And I can’t wait until the day when I have the privilege of seeing my students experiencing those same moments of clarity and comprehension, exhilaration and accomplishment.”

Working with other colleagues, particularly Mercedes McGowen, formerly at William Rainey Harper College in Chicago,  we find that teaching this way – focussing on connections between different mathematical problems – we cannot “teach” students to see connections.

We can set up conditions under which their sudden enlightenment is more likely, but ultimately it is not a matter of learned behavior, rather of the students’ direct noticing and seeing. These moments of vision on the part of students are usually accompanied by expressions of intense pleasure and wonder.

It is those moments we seek to capture and to highlight, to refer our students back to “when you saw …”. This gives our students the possibility of a new way of understanding mathematics, and a new way of remembering.

Those who have clear visions of connections, and who forge strong episodic memories no longer see mathematics as a collection of unrelated facts and formulas. Things make sense for them, and it is exactly the memory of the sense-making that constitutes what mathematics is for them now.

The advantages of this are enormous – instead of mathematics being laborious and hard to remember, it is now easy and pleasurable. So we now teach to foster such memories: strong, vivid, episodic memories of seeing connections between different parts of mathematics.