No surprise to anyone really that students get confused by the difference between definite and indefinite integrals. The so-called indefinite integral is not really an integral at all, not in the sense of area: it’s the solution set to a differential equation. It’s not even usually a single function at all, but a whole family of functions.

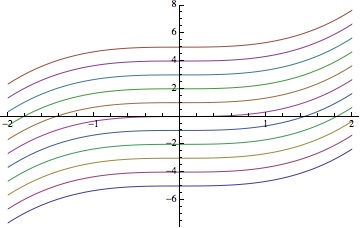
To imagine that defines a single thing – a function for which   – is to miss the important point that this differential equation has a whole family of solutions: , a  solution for each real number :

So, , NOT  as is commonly written.

The villain who engendered this confusion was none other than the great Gottfried Wilhelm Leibniz a co-discover/inventor of calculus along with Isaac Newton.

Wait! I hear you say, isn’t this just pedantry? Does it really matter if we write  as or as the fashionable set-theoretic  ?

Well yes, it does. Think about how you might resolve the following apparent conundrum:

so !!

This is nonsense, of course, because the algebraic calculation proceeds as if  is a well-defined function, which it is not: it is a family of functions (even worse – defined over a disconnected domain).

Students of mathematics need to learn how to think, not carry out mindless calculations as if they were performing monkeys.

This is an important psychological point: students are used to writing  as a conditioned response, functioning at a symbolic level equivalent to that almost of a dog or a cat (“sit, Fido”, “Here’s food, puss.”), whereas to gain mathematical power and flexibly they need to be functioning at a much higher symbolic level, utilizing a far richer collection of symbolic reference.