What do we need to solve quadratic equations?
Posted by: Gary Ernest Davis on: June 11, 2011
Completing the square
A former colleague wondered if the quadratic formula held when
are complex numbers.
He could, of course, have figured this out by the process of completing the square:
If then
exactly when
(thanks to James Tanton for this trick).
This happens exactly when or, equivalently when
.
This leads us to the equivalent form from which we deduce the quadratic formula.
What allows this to work?
What did we need to get this line of reasoning to work?
- We need to know that if
then
exactly when
. This means we can multiply and divide by non-zero quantities (as well as add and subtract).
- In exchanging
for
we are using commutativity of multiplication. We use this again in expanding the square
In current mathematical parlance, this means the quantities come from a field. Examples are the field of rational numbers, the field of real numbers, and the field of complex numbers.
Square roots
To take the final step from to
we need to be able to extract square roots. In the field of real numbers we can always do this for non-negative numbers, but already the field of rational numbers presents difficulties. For the complex field we can always solve
for
but the square root function does not exist as it does for positive real numbers.
A finite field
The numbers  where we add and multiply modulo 7 – keeping only the remainder after division by 7 – form a field, denoted
The only point that might be in doubt is division by a non-zero quantity, but we can see this can always be carried out from the following table of multiplicative inverses:
| x |
reason |
|
| 1 | 1 | |
| 2 | 4 | |
| 3 | 5 | |
| 4 | 2 | |
| 5 | 3 | |
| 6 | 6 |
So to solve a quadratic equation where the quantities
come from
we can reach the step
and then wonder if we can always solve this equation.
For example if try to solve the quadratic equation where
come from
we reach the step
mod 7.
What solutions, if any, are there to mod 7?
| x | |
| 1 | 1 |
| 2 | 4 |
| 3 | 2 |
| 4 | 2 |
| 5 | 4 |
| 6 | 1 |
So there are two solutions for to
:
.
This gives or
so that
or
Quadratic residues
We can replace the number 7, above, by any prime number to get a field denoted
.
The existence of multiplicative inverses follows from Euclid’s algorithm, and when is not a prime number it’s easy to see that division by non-zero quantities in
is not always possible.
When the equation has a solution in , the number
is called a quadratic residue mod p.
Determining which numbers are quadratic residues mod p is a solved, but interesting, problem that is an excellent investigation for students, and it comes simply out of trying to solve quadratic equations over these fields.
Finite fields
But this does not exhaust the finite fields, and for every prime number and positive integer
there is a field – known as a Galois field – with
elements.
So now we want to know under what conditions we can solve where
come from a finite field.
Rational numbers
When the quantities are rational numbers we again have the question of whether the equation
has a rational number solution for
This, of course boils down to when has a rational number solution when
is a rational number – that is, to when square roots of positive rational numbers are again rational numbers.
The moral?
Thinking about exactly what we need to solve a quadratic equation leads us straightforwardly to solving quadratic equations over less often encountered number fields, which in turn leads us directly to interesting and deep questions of number theory, which, nevertheless, are capable of being investigated by school students.
Investigating quadratic residues mod p, p prime, might also lead to more respect for the subtle intricacies of the square root as a function. The answer to is not resolved by simply writing
.
5 Responses to "What do we need to solve quadratic equations?"
Fascinating stuff. My reaction to the first question was obviously it’ll hold for complex numbers – just use de Moivre’s formula. Sometimes the answer isn’t so clear cut!
Btw, you left off a square on the first x in 4a^2x+4abx+4ac=0 (3rd paragraph) and the square brackets in [2ax+b]+4ac-b^2=0 in the 4th paragraph should also be squared. :)
Interesting article as always. I personally don’t have a problem with using the quadratic formula when a,b,c are complex numbers. Here’s why. Let d denote the discriminant d=b^2-4a. As to whether or not the quadratic formula makes sense for coefficients a,b,c in some number system K is as follows:
Does the equation z^2=d have two distinct roots in K for any choice of d in K? Is one root always -1 times the other? The answer for the complex numbers is yes (e.g. fundamental theorem of algebra, de moivre’s theorem).
In fact, this raises an interesting point about inverse functions vs multifunctions. We restrict our domain in a canonical way to make the inverse a function by taking the canonical choice of root with argument (for example) at least 0, strictly less than pi. But this is exactly what we do in the real case, so there’s very little difference.


June 12, 2011 at 1:08 am
I love the idea of investigating the extent of the generality of an important result with teachers and students! “Under what circumstances will this stay true?” is a great question that I am drawn to the idea of adding to the basic repertoire of school math.
… But wait, since you brought in finite fields, isn’t there one other detail needing consideration?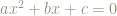 always implies
always implies  , but the latter does not imply the former if it so happens that 4=0, which is true if the field is characteristic 2, for example
, but the latter does not imply the former if it so happens that 4=0, which is true if the field is characteristic 2, for example 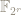 or the function field
or the function field 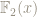 . So doesn’t the quadratic formula require that the characteristic of the field is not 2?
. So doesn’t the quadratic formula require that the characteristic of the field is not 2?
June 12, 2011 at 7:44 am
Yes, you’re right: characteristic 2 is almost always a special case.
We do not have to use Jim Tanton’s trick, and can proceed as usual to complete the square. However we still have to be concerned about the characteristic 2 case when we attempt to divide by 2.
Thanks for pointing it out.