If you think mathematics is just a language, seek ponder this:

and think again.

Courtesy of Chris Budd & +plus magazine

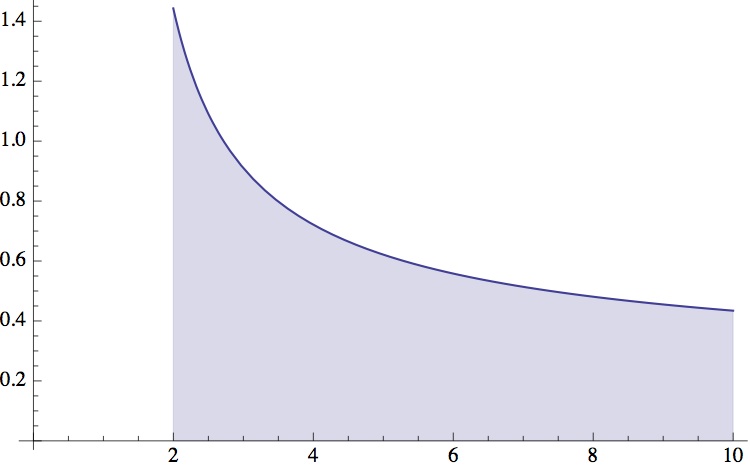
And if, see perchance,  that is not convincing enough, try this: for a positive real number let denote the number of primes less than or equal to , and let be the area, from 2 to , under the graph of :

Area under curve  from t=2 to t=x (here, x=10)

Then:

The rate at which  approaches 1 is a major area of mathematical research, which is not advanced one whit by the view that mathematics is a language.