The Rascal Triangle: how magic can happen if you listen to kids

Posted by: Gary Ernest Davis on: January 8, 2011

In: Uncategorized
Comment!

0 Shares

Three middle school students, widely geographically separated, worked together to produce a novel piece of mathematics of interest.

The students, shown above, are (from left to right):

Alif Anggoro, a seventh grader at Al Azhar Junior High School in Java Bekasi, Jakarta, Indonesia
Eddy Liu, an eighth grader at Washington Middle School, Seattle, Washington, USA
Angus Tulloch, an eighth grader at Crestomere School in Rimbey, Alberta, Canada

The results of their original work are here: The_Rascal_Triangle

In this post I want to discuss what they did, how they came to do it, and what lesson their might be in their experience for mathematics education.

This is a perfect story to report on in the Republic of Mathematics, because it shows that when kids are listened to they can have tremendous fun working out their own ideas.

It also shows that just because someone is young and in middle school does not mean that they cannot think with maturity, given half a chance.

What did they do?

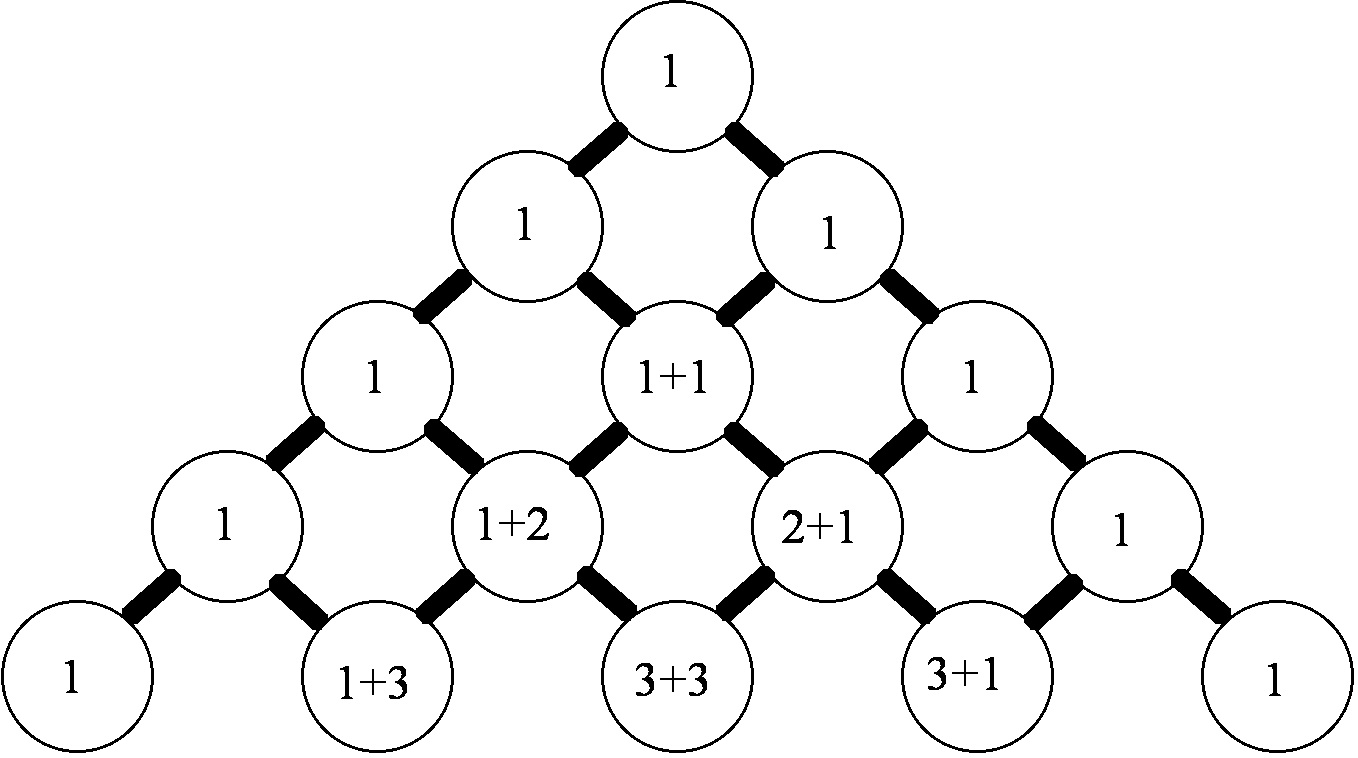
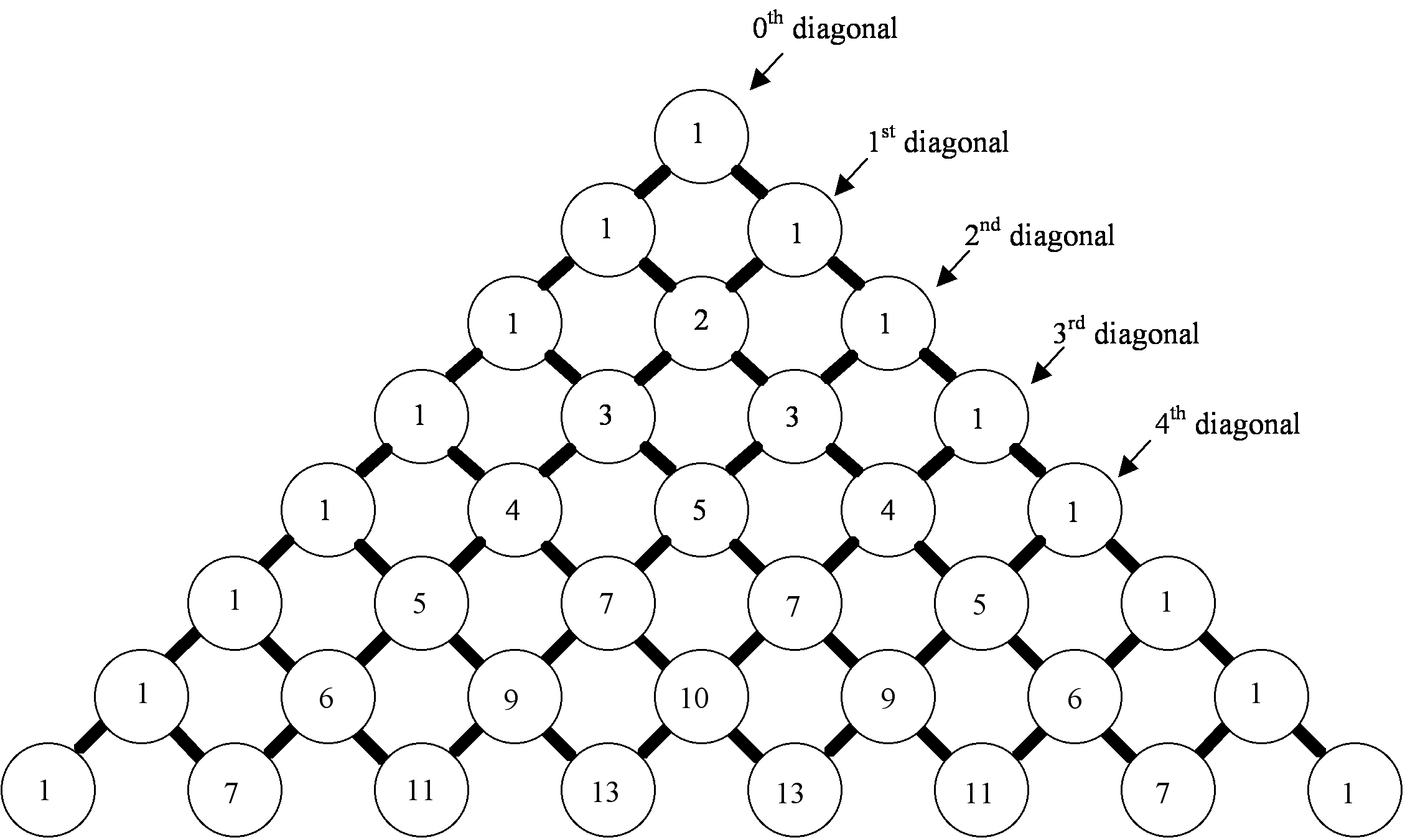
These three middle school students built a version of Pascal’s triangle – which they named The Rascal Triangle – by using a different rule for producing numbers in a row of the triangle from the row above.

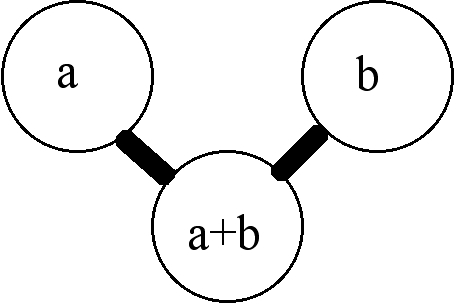
In Pascal’s triangle the entries, other than the 1’s, are obtained from the two entries above, to the left and right, by addition:

First 5 rows of Pascal's Triangle

Pascal’s triangle does not stop at row 5, but goes on forever.

The general scheme for determining entries in Pascal’s triangle, other than the outside 1’s, can be represented as follows:

The rule for generating Pascal's Triangle

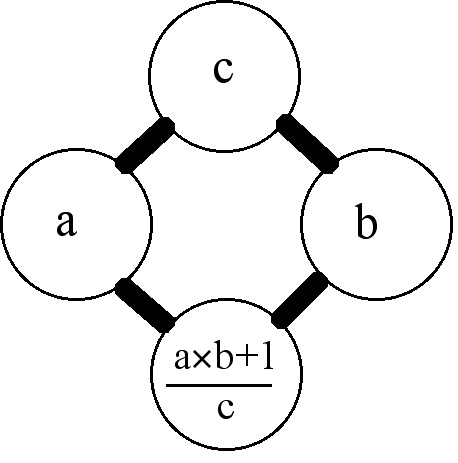
Alif, Eddy and Angus came up with a different rule for determining entries in the otherwise blank triangle:

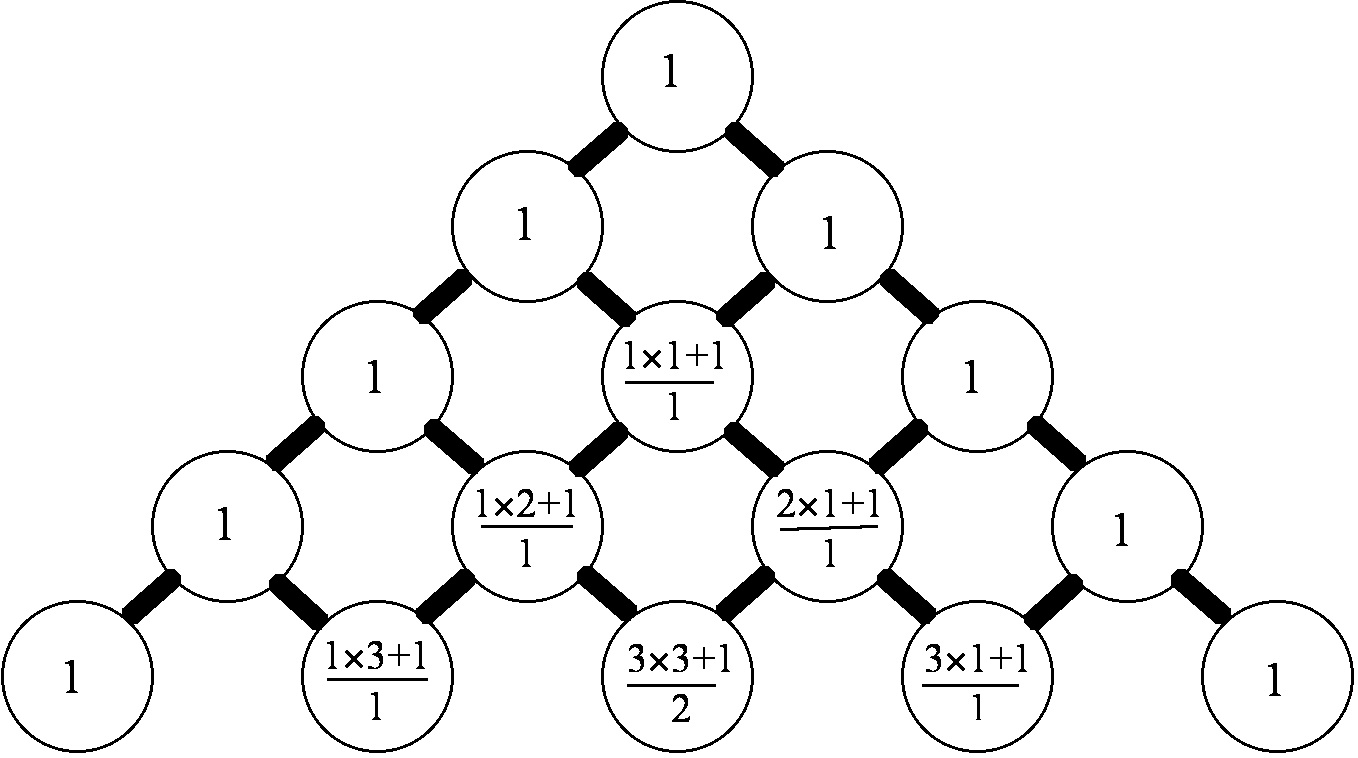
This generates the Rascal Triangle:

First 5 rows of the Rascal Triangle

Like Pascal’s Triangle, the Rascal Triangle does not stop at row 5 but goes on forever.

However, unlike Pascal’s Triangle, the middle entry in row 5 of the Rascal Triangle is 5, not 6.

The challenge for the students was to show that the entries in this Rascal Triangle are whole numbers, which is not at all obvious from the generating rule for the Rascal Triangle.

A fuller version of the Rascal Triangle shows an interesting pattern along the diagonals:

Patterns along the diagonals of the Rascal's Triangle

The $2^{nd}$ diagonal, for example consists of the numbers 1, 3, 5, 7, 9, 11Â … Starting from 1, these numbers are spaces 2 apart.

The $3^{rd}$ diagonal consists of the numbers 1, 4, 7, 10, 13, … . Starting from 1, these numbers are 3 spaces apart.

The $4^{th}$ diagonal consists of the numbers 1, 5, 9, 13 … Starting from 1, these numbers areÂ 4 spaces apart.

It’s a decent guess, therefore, from as much of the Rascal Triangle as we can see, that the entries on the $m^{th}$ diagonal are $1, m, 1+2m, 1+3m, 1+4m, 1+5m, \ldots$ .

If we count the beginning 1 in this sequence as the $0^{th}$ term then this guess as to the diagonal entries would say that the $n^{th}$ term on the $m^{th}$ diagonal is $m\times n +1$ .

If this guess is correct then the Rascal Triangle does indeed have only whole number entries.

To establish this pattern guess is indeed correct, imagine a triangle in which, in fact, theÂ $n^{th}$ term on the $m^{th}$ diagonal is $m\times n +1$ . In particular, the beginning entry in each diagonal is 1.

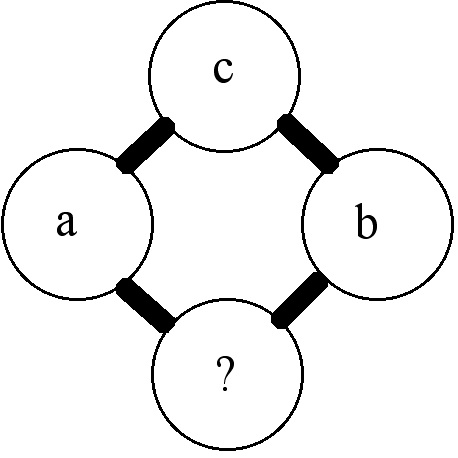
We can show this must be just the Rascal Triangle if we can show that such a triangle has the same generating formula as the Rascal Triangle.

In the diagram above, suppose that the $c$ entry is the $n^{th}$ entry on the $m^{th}$ diagonal, so that $c=mn+1$ .

Then $a$ is the $(n+1)^{st}$ entry on the $m^{th}$ diagonal, so $a=m(n+1)+1$ .

Also, $b$ is the $n^{th}$ entry on the $(m+1)^{st}$ diagonal so $b=(m+1)n+1$ .

And finally, the ? entry is the $(n+1)^{st}$ entry on the $(m+1)^{st}$ diagonal so $?=(m+1)(n+1)+1$ .

Then,

$\frac{a\times b+1}{c}=\frac{(m(n+1)+1)\times ((m+1)n+1)+1}{mn+1}$

$=\frac{(mn+m+1)\times(mn+n+1)+1}{mn+1}$

$= \frac{m^2n^2+m^2n+mn^2+3mn+m+n+2}{mn+1}$

$= \frac{mn(mn+1)+m(mn+1)+n(mn+1)+2(mn+1)}{mn+1}$

$=mn+m+n+2 = (m+1)(n+1)+1=?$

so , indeed the Rascal generating rule holds for this triangle, so it IS the Rascal triangle, and therefore the Rascal Triangle has whole number entries

Why did they do it?

In the write-up of their joint work the students construct a hypothetical scenario in which a teacher gives them an “IQ test” question to fill in the $5^{th}$ row of a triangle by guessing the pattern from the previous rows.

The students guess the middle term of the row is 5 because they have a rule that corresponds to the Rascal Triangle.

The hypothetical teacher then says that this rule is complicated and anyway may not give whole number answers, so the students set out to show that whole number answers result.

In fact, the real situation was quite different.

Liu is an eighth-grader at Washington Middle School in Seattle, Washington. He served as the corresponding author for the paper. Tulloch is an eighth-grader at Crestomere School in Rimbey, Alberta. Anggoro, a seventh-grader at Al Azhar Junior High School in Java Bekasi, a suburb of Jakarta, Indonesia, has never met his fellow authors. Their collaboration was conducted via email.

Mathematician Andy Liu (University of Alberta) orchestrated the collaboration. Eddy Liu, Andy’s nephew, first met Tulloch at a mathematics summer camp in Edmonton in 2008. “I met Alif in Manila during the First EastÂ Asian Mathematics Summer Camp in 2009,” Andy Liu wrote in a recent email. “At that time, Eddy and Angus had been working on the triangle problem. However, like typical North America cars, their engines were not highly charged, but their brakes were mighty powerful. So I suggested to Alif to contact both Eddy and Angus, which he took the initiative to do so.” (Mathematical Association of America, 2010)

What lessons are there for mathematics education?

The MAA web page indicates that Andy Liu had a strong hand in guiding the students to work together.

What is not clear from that account, or from the students final article, is how they really came to work on the problem, and how much help Eddy Liu’s uncle Andy gave along the way.

After reading the published article I believe that a relatively sophisticated mathematician wrote most of the argument. This is not to say that the students did not come up with, or understand, the argument. However, the language is, in my experience quite sophisticated for middle school students, the algebra is quite complicated for middle school students, and the argument to show that two inductively defined objects are equal when the satisfy the same generating formula and the same boundary conditions is very sophisticated for school students.

I would dearly like to know the dynamics of the solution to this problem because it is a beautiful example of what can motivate students in mathematics.

It is a lovely example of how much fun school mathematics can be if a teacher – in this case probably uncle Andy Liu – listens to students and encourages and nurtures their ideas.
What tremendous pride these 3 students must feel to see their work written up in print for the world to see.

Congratulations to them and uncle Andy Liu on a beautiful example of how middle school students can do interesting mathematical research.