The distributive property
Posted by: Gary Ernest Davis on: January 10, 2010
This post is about the following fact: for whole numbers
.
Sometimes this is called the distributive property of multiplication over addition, and sometimes it is called the distributive law. Some people are uncomfortable with use of the word “law”, as if it were passed by fiat and we darned well better follow it or else. Â That’s not what the word “law” means in mathematics, but to avoid those sort of associations, let’s just call it the distributive property.
In the set of natural numbers the distributive property can be proven true from the standard Peano axioms.
However, school mathematics does not deal with natural numbers. That comes later, in college, when students learn about foundational issues in mathematics, such as what are sets, axioms for sets, axioms of infinity, and so on. Â In school we deal with the counting numbers .
What we know about the counting numbers has to come from acts of counting, not by inductive proof. So the distributive property in school mathematics needs to be placed in the context of counting, since we are dealing, in school , with counting numbers, a much less formal notion than natural numbers.
A simple version of the distributive property is for all counting numbers
.
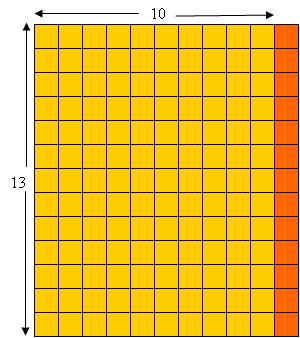
This simple version of the distributive property has a very nice, simple interpretation in terms of units of the number “a”. To illustrate this through a concrete example, let’s look at :
Here, as adults, we can see the column of 13 small squares as a unit that is repeated 11 times. The very simple form of the distributive property says that we can split off 1 of those units, and count 10 lots of the unit 13, and then add in the extra unit of 13. Sort of obvious when you see it this way.
However, many children, even in grades 3-6, are not entirely stable or comfortable counting in units. Often young children, 6 years old, will recite count by 2’s: , … If they are able to do this they will happily show you that they can do so.
However, they may not yet be able to count by units of 2. For example, if a child can recite by 2’s, tell them you were counting by 2’s to 24 and ask them how many times you counted. Some children, not all, will answer 12, usually tapping two fingers as they count, or perhaps nodding their head as they recite 2’s. These children are counting their acts of reciting by 2’s, and are able to count by units of 2. The ability to do this develops gradually, and by grades 3-6 most, but not all, children will be confident counting by units. If they are not, the distributive property is going to cause them some difficulty.
Additionally, young children, in grades 1- 3, often cannot see rectangular arrays the way adults see them: as repeated rows, or repeated columns, where the rows, or columns, are themselves built from repeated squares.
Seminal studies by Lynne Outhred and her doctoral adviser Michael Mitchelmore show convincingly the developmental steps involved in young children’s ability to recognize and reproduce rectangular arrays as repeated rows of repeated squares. Here is an example from a paper of theirs [Student’s_structuring_of_rectangular_arrays] which illustrates some of the development steps children go though in being able to communicate in a drawing what constitutes an array:
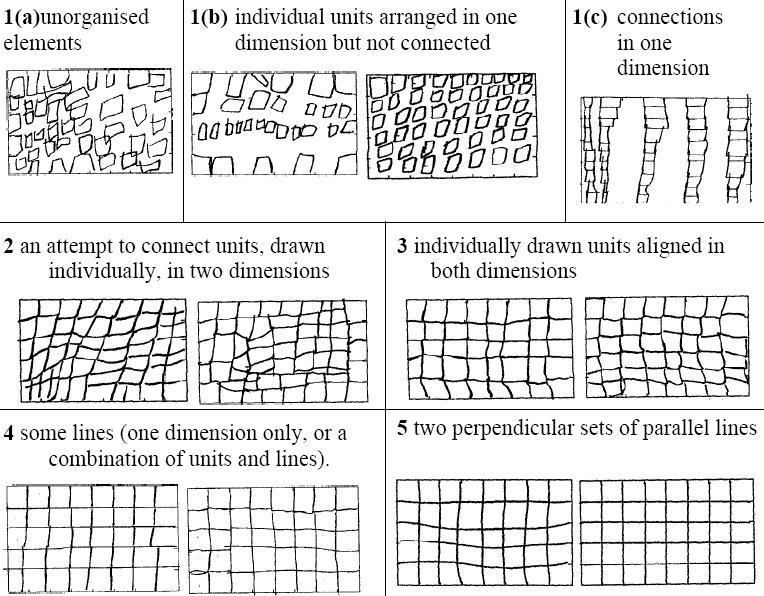
So this simple form of the distributive property, so clearly illustrated for an adult by a rectangular array, may not be so clear to a child who (a) is not yet confidently counting by units or (b) is still developing the skill of seeing a rectangular array as composed of rows and columns.
As adults we take these two developmental skills for granted, because it’s hard to imagine a time when we did not have them. But clearly, at age 1 month we did not, and somewhere before age 21 years we probably did. These skills did not just pop into our heads fully formed, so we went through a period of developmental in gaining these skills. So, do all children. Â It is advantageous for us, as parents and teachers, to figure out where children are before we begin “explaining” the distributive property to them.
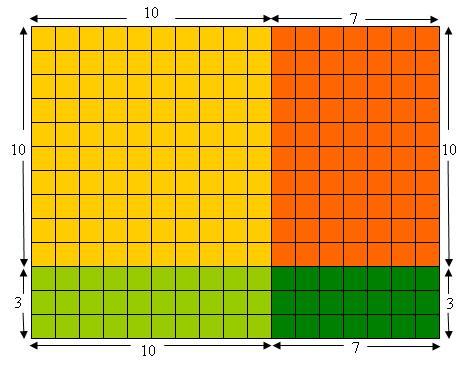
The more general distributive property  also has a simple interpretation in terms of rectangular arrays – simple for an adult that is.  Here is an array decomposition illustrating
:
Repeating the distributive property allows us to see that for all counting numbers we have
.
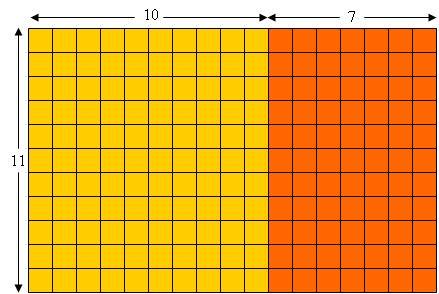
Again this can illustrated nicely by a decomposition of a rectangular array. For example, here’s an array decomposition illustrating :
But we have to bear in mind, As I wrote above, that just because these are  simple and compelling explanations of the distributive property for us, as adults, it does not follow that a child will have the necessary skills to see what we see so clearly.
The distributive property is very important for algebra. One reason is because of its applications, for example in multiplying binomial expressions . Another reason is that a grasp of the distributive property is a good indication of a student’s number sense and that, in turn, is an excellent indicator of how readily a student can grasp algebraic ideas.


June 17, 2010 at 9:22 pm
I made a video that shows the “freshman dream” aka the biggest mistake kids (and adults!) make when using the distributive property. I’d like to make another video showing that distribution is just a fast way to ass a bunch of (a+b)’s. I’ll get to that one at some point!
http://zerosumruler.wordpress.com/