Jim Tanton (@jamestanton ) Tweeted:

“x=-b/(2a) ugh!For y=3x^2-12x+7 factor first 2 terms y=3x(x-4)+7 See x=0 & x=4 give same output. Axis of symm must be x=2.Try this on y=ax^2+bx+c!”

This, in my experience, is a simple yet typical example of Jim’s thinking: highly relational and generally avoiding instrumental procedures.

In this post I simply want to elaborate on this idea.

A quadratic polynomial function is symmetric about some line . Also, is either entirely increasing, or entirely decreasing, to the left of the line of symmetry, and to the right of the line of symmetry it is doing the opposite:

Students are often – usually? – taught that the axis of symmetry is without any rhyme or reason.

Knowing this is “knowledge that” something is so, without any relational understanding of why: students can “know that” without “knowing why”. Richard Skemp elaborated on the differences between relational and instrumental understanding, and his article is worth reading (again) in this context.

Let’s look in more detail at Jim Tanton’s example, above.

The quadratic polynomial can be written as . This simply results from the common factor of “” in and .

We can make the term equal to 0 in two ways: by making and by making .

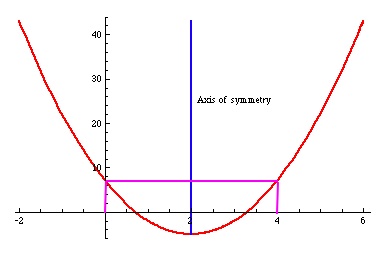
For both these values, , we have .

In other words, at the function takes the same value (namely, 7).

Because is symmetric about some line , and decreasing/increasing differently on opposite sides of the line of symmetry,  this axis of symmetry occurs midway between , that is, at :

Let’s take another example: the quadratic polynomial .

Using Jim Tanton’s idea we factor from the first two terms to get .

From this we see, as before, that .

Again, because the quadratic polynomial is symmetric about a vertical line and decreasing/increasing differently each side of that line, the line of symmetry is .

Applying this idea to a general polynomial , where we see that so the axis of symmetry is midway between , that is at

Richard Skemp

Instrumental “understanding” involves being able to follow a set of instructions without knowing why you are doing so.

Relational understanding involves understanding the relationship of one thing to another to help guide you to a correct conclusion.

As Richard Skemp points out, relational understanding sometimes takes a little more mental effort to get what is going on, but pays off in terms of both flexibility, and a feeling of genuine understanding, stemming from seeing the relationship between various things.