Why Jared and Brittany will never be good at math.1
Posted by: Gary Ernest Davis on: September 15, 2013
Jared “simplified” in algebra class.
His math teacher asked how he got that. “Easy!” said Jared. “Just cancel the x’s.” Jared was pretty sure he was becoming skilled at canceling.
“But what if you put intoÂ
?” the teacher asked Jared. “The result would be 2, not 1.”
Brittany jumped into the conversation: “You can’t do that, because x isn’t a number.”
Jared nodded enthusiastic agreement. “That’s it,” he said. ‘This is algebra, and x is – part of algebra. It’s not a number, like Brittany says.”
“But it is a number,” Â replied the teacher.
“Well what number is it?” asked Brittany.
“No, no,” said the teacher. “It’s not any particular number. It stands for a possible number. It’s a variable”
“Then what possible number does it stand for?” asked Jared, getting into the swing of it.
“How can it be a number if it’s a variable?” asked Brittany (dripping with sarcasm).
They knew their math teacher was a little odd, but even they were surprised when she banged her head hard, several times, against the wall, and walked out of the room
When is an integral not an integral?
Posted by: Gary Ernest Davis on: September 14, 2013
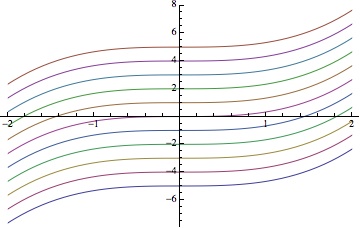
No surprise to anyone really that students get confused by the difference between definite and indefinite integrals. The so-called indefinite integral is not really an integral at all, not in the sense of area: it’s the solution set to a differential equation. It’s not even usually a single function at all, but a whole family of functions.
To imagine that defines a single thing – a function
for whichÂ
 – is to miss the important point that this differential equation has a whole family of solutions:
, a  solution for each real number
:
So, , NOTÂ
as is commonly written.
The villain who engendered this confusion was none other than the great Gottfried Wilhelm Leibniz a co-discover/inventor of calculus along with Isaac Newton.
Wait! I hear you say, isn’t this just pedantry? Does it really matter if we write as
or as the fashionable set-theoreticÂ
?
Well yes, it does. Think about how you might resolve the following apparent conundrum:
so
!!
This is nonsense, of course, because the algebraic calculation proceeds as if is a well-defined function, which it is not: it is a family of functions (even worse – defined over a disconnected domain).
Students of mathematics need to learn how to think, not carry out mindless calculations as if they were performing monkeys.
This is an important psychological point: students are used to writing as a conditioned response, functioning at a symbolic level equivalent to that almost of a dog or a cat (“sit, Fido”, “Here’s food, puss.”), whereas to gain mathematical power and flexibly they need to be functioning at a much higher symbolic level, utilizing a far richer collection of symbolic reference.