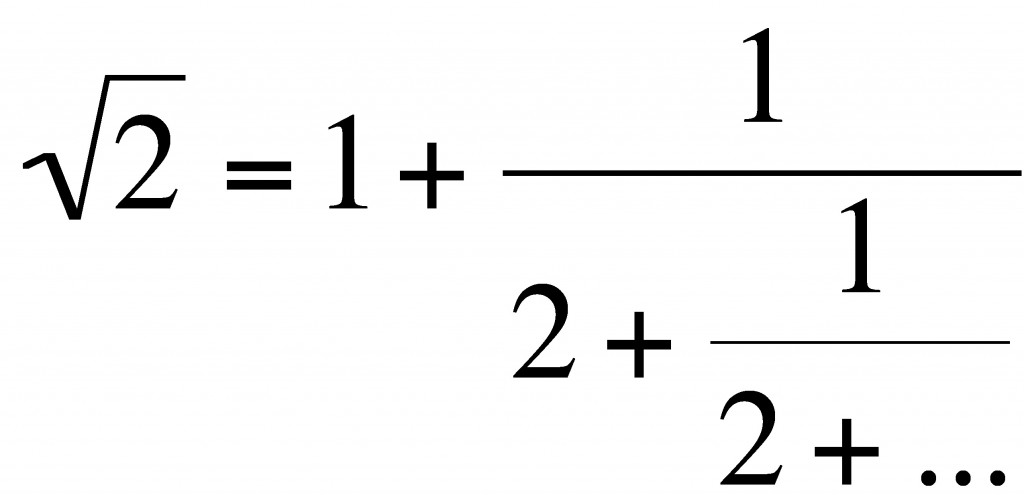Republic of Mathematics blog

Is rationalizing rational?

Posted by: Gary Ernest Davis on: May 3, 2011

In: Uncategorized
8 Comments

Rationalize or get it wrong?

Text books and test setters regularly mark students wrong if they give an answer of $\frac{1}{\sqrt{2}}$ to a problem.

A student is supposed to know, as part of mathematical convention, that $\frac{1}{\sqrt{2}}$ should be rationalized to $\frac{\sqrt{2}}{2}$ .

This issue has been discussed before by @suburbanlion at SuburbanLion’s Blog and @jamestanton at Rationalising the Denominator, among others.

Marking a student wrong for not carrying out a rationalization like this is just BS (and I don’t mean “Bachelor of Science”).

And there is no such mathematical convention – it’s made up by people who write text books and set tests.

This issue came up again recently in #mathchat when @davidwees wrote: “I tell my students that people used to rationalize denominators b/c it made calculations easier” and “1.414…/2 is much easier to do than 1/1.414… without a calculator.”

My issue with what David wrote (and indeed with part of what James Tanton says in his video) is how, without a calculator, do we know that $\sqrt{2}\approx 1.414$ ?

Of course if someone told us that $\sqrt{2}\approx 1.414$ and we figured that $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ then we could probably be adept enough to calculate $\frac{1}{\sqrt{2}}\approx 1.414/2=0.707$ by hand.

The field $\mathbb{Q}[\sqrt{2}]$

Numbers of the form $a+b\sqrt{2}$ where $a \textrm{ and }b$ are rational numbers (fractions) collectively have a remarkable structural property:

not only can we add, subtract and multiply such numbers and still get numbers of the same form (e.g. $(1+2\sqrt{2})\times (2-3\sqrt{2})=-10+\sqrt{2}$ ), we can also divide such numbers and still get a number of the same form:

e.g. $\frac{1+\sqrt{2}}{2-3\sqrt{2}}= \frac{1+\sqrt{2}}{2-3\sqrt{2}}\times \frac{2+3\sqrt{2}}{2+3\sqrt{2}}=\frac{14+7\sqrt{2}}{-14}=-1-\frac{1}{2}\sqrt{2}$

Collectively, numbers of the form $a+b\sqrt{2}$ constitute a mathematical field, denoted by $\mathbb{Q}[\sqrt{2}]$ – a structure in which addition, subtraction, multiplication and division (by non-zero numbers) is always possible.

From this perspective, rationalizing $\frac{1}{\sqrt{2}}=\frac{1}{2}\sqrt{2}$ is just expressing the fact that the reciprocal of $\sqrt{2}$ is again in the field $\mathbb{Q}[\sqrt{2}]$ .

What about rational approximations?

There are technical senses in which the continued fraction of a real number gives the “best” rational approximation to that number.

So how do we find the continued fraction for $\sqrt{2}$ ?

We are looking for an (infinite) expression of the form :

$\sqrt{2}=a_0+\frac{1}{a_1+\frac{1}{a_2+\ldots}}$

where the $a_n$ are whole numbers.

Because the piece $\frac{1}{a_1+\frac{1}{a_2+\ldots}}$ after $a_0$ is less than 1, we see that $a_0$ is the largest integer less than $\sqrt{2}$ , which is 1 (we know $1< \sqrt{2} < 2$ because $1=1^2 < 2=\sqrt{2}^2 < 4=2^2$ ).

This leaves $\frac{1}{a_1+\frac{1}{a_2+\ldots}}= \sqrt{2}-1$ so taking reciprocals we see that $a_1+\frac{1}{a_2+\ldots} =\frac{1}{\sqrt{2}-1}$ .

This means that $a_1$ is the largest integer less than $\frac{1}{\sqrt{2}-1}$ .

In other words, $a_1<\frac{1}{\sqrt{2}-1}<a_1+1$ , which means that $1+\frac{1}{a_1+1}<\sqrt{2} < 1+\frac{1}{a_1}$ .

We know $1+\frac{1}{3} <\sqrt{2} < 1+ \frac{1}{2}$ because $(1+\frac{1}{3})^2=\frac{16}{9} < 2 <\frac{9}{4}= (1+ \frac{1}{2})^2$ , so $a_1=2$ .

Continuing in this vein gets trickier, because next we have to find the largest integer less than $\frac{1}{\frac{1}{\sqrt{2}-1}-2}$ .

Because $\sqrt{2}$ satisfies a quadratic equation we can use a cute trick to find the continued fraction for $\sqrt{2}$ .

Let’s write $\alpha = \sqrt{2}+1$ so that $\alpha^2=(\sqrt{2}+1)^2=2+2\sqrt{2}+1=2\alpha+1$ .

Dividing by $\alpha$ gives:

$\alpha = 2+\frac{1}{\alpha} = 2+\frac{1}{2+\frac{1}{\alpha}}=2+\frac{1}{2+\frac{1}{2+\frac{1}{\alpha}}}$

Taking this to a limit we get $\alpha = 2+\frac{1}{2+\frac{1}{2+\ldots}}$ .

Since $\sqrt{2}=\alpha - 1$ we get $\alpha = 1+\frac{1}{2+\frac{1}{2+\ldots}}$ .

By successively terminating this continued fraction we get the following rational approximations to $\sqrt{2}: 1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12},\frac{41}{29}$ .

This immediately gives us the following rational approximations to $\frac{1}{\sqrt{2}}: \frac{2}{3}, \frac{5}{7}, \frac{12}{17},\frac{29}{41}$ .

Newton and the Babylonians

Image courtesy Bill Casselman

Isaac Newton’s method for finding roots of functions, applied to the polynomial $x^2-2$ leads directly to a method for approximating $\sqrt{2}$ known to the Babylonians.

Using this method we start with an approximation $x_0$ – let’s start with $x_0=1$ because its the first approximation from the continued fraction for $\sqrt{2}$ : it’s the integer part of $\sqrt{2}$ .

We then average $x_0 \textrm{ and } \frac{2}{x_0}$ to get the next approximation $x_1$ .

We generate a sequence of rational number approximations $x_n$ to $\sqrt{2}$ where. at each step, $x_{n+1}=\frac{1}{2}(x_n+\frac{2}{x_n})$ .

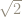This gives us the following rational number approximations to $\sqrt{2}: 1, \frac{3}{2}, \frac{17}{12},\frac{577}{408}$ .

$\sqrt{2}$ as a decimal

So now we know how to approximate $\sqrt{2}$ by rational numbers, we can use the rationalization $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ to get rational approximations to $\frac{1}{\sqrt{2}}$ , but you see the absurdity – why bother? Just invert the rational approximations to $\sqrt{2}$ .

How about the decimal expansion of $\sqrt{2}$ – where does that come from?

Decimal approximations to $\sqrt{2}$ are usually obtained from the rational approximation from the continued fraction, of from the more rapidly convergent Newton’s (= Babylonian) method.

The record at the time of writing this post isÂ is 1,000,000,000,000 decimal places due to S. Kondo & A.J. YeeÂ in 2010.

The empirical evidence is that $\sqrt{2}$ is normal in base 10, meaning that, to date, each of the digits appears with proprtion $\frac{1}{10}$ , each pair of digits with proportion $\frac{1}{100}$ , each triple of digits with proportion $\frac{1}{1000}$ and so on.