Computational media: the universal acid of mathematics teaching (5)
Posted by: Gary Ernest Davis on: January 4, 2010
Nigel Smith was a teacher at Twyford Preparatory School, Winchester, England. He was my friend and colleague. He died of brain cancer at age 44, 8 years ago. I still miss him deeply and I want to write about some things we did together in his class at Twyford.
I met Nigel when he enrolled as a graduate student in education at the University of Southampton, where I was Professor of Education. Â Nigel and I hung out quite a lot. We drank together, at home and at local pubs, and had long conversations about mathematics teaching. Many of these were with another colleague, David Hill, who taught mathematics at Hordle-Wallhampton School near Lymington where Nigel was previously Head of Mathematics. Â The three of us would go to David’s house and then walk a few hundred yards to his local pub, the Chequers Inn, for lunch. We ate, drank, walked and talked. We wrote articles together, and enjoyed each others company.
Nigel taught grades 5 through 8 at  Twyford, which is a “prep” school. What this means is that children at Twyford were being prepared, or “prepped”, to enter the competitive private schools – known as public schools in England – such as Eton, Rugby and Winchester. Parents pay large sums of money to send their children to prep schools, and teachers are expected to obtain good results. This means, in practice, success in getting students into the major public schools. Nigel was good at his job, and his students regularly scored very well on admission tests. His continuing employment depended on his ability to get his students through these admissions tests.
Yet Nigel did not simply “prep” his students in test-taking. In fact he did this relatively rarely. What he did do, a lot, was to make mathematics interesting, fun and exciting for his students. He did this by experimenting with investigations, some of which we worked out together.
Nigel’s Head-teacher – his Principal to U.S. readers – Â asked the IT teacher who at Twyford was most innovative in the use of technology in their teaching. The IT teachers’ response was: Nigel Smith. Yet Nigel could barely make his way around Microsoft Word, so how did he get this – well-deserved – reputation?
Nigel used technology because it furthered his aim of creating an open, questioning approach to learning mathematics.
I recall several examples of the use of technology to further his aims of  mathematical investigations. These, as I recall, were  used with grades 7 and 8:
(1) Data analysis using Excel
Nigel had devised an investigation, the details of which escape me, involving a tortoise and hare race. Students did calculations – by hand – and plotted the resulting data in Excel, looking for straight line and quadratic fits to the data.
(2) Conway’s Game of Life
I introduced Nigel to Conway’s Game of Life and he was bowled over by it. Â He thought it an excellent vehicle for investigation and reasoning. Nigel gave the students a few starting points and then let them play for the first lesson. He set as homework the problem to explain why gliders glide. Anyone can see that they glide. Nigel’s question was: why?
Nigel’s students worked at creating complex eventually-periodic cellular automata, some of them with periods on the order of several hundred.
I was in Nigel’s class one day when the Head-teacher brought parents of a prospective student into the room to show them features of the mathematics program. The Head teacher and parents approached me and asked what the boy next to me was doing. I said: ” Why don’t you ask him?” Â This boy then explained in a most articulate way, how they were investigating repeating cellular automata, of which the glider was a simple example. The Head-teacher and visitors left very impressed.
(3) Secret codes
Nigel and I discussed a lesson sequence based around simple ciphers. Our aim was to introduce the students to the use of modular arithmetic in a practical setting of devising and cracking secret codes, beginning with simple substitution codes. Â The students loved this activity. They worked in small teams, competing one against the other, encoding and trying to crack the coded messages. They used Excel to carry out modular arithmetic, and code their message.
At Christmas break we gave the teams an exercise to set a reasonably long coded message for other teams to try to crack over the break. I explained to the students that most coded messages were not cracked by intelligent application of decoding  skills, but rather by breach of protocol or by coercion. A student asked what that meant. I explained breach of protocol as not following the set procedure for coding, using Alan Turing and others’ cracking of a German code as a result of a breach of protocol.  I explained coercion through the example of torturing someone who you knew held the key to the code. At that point, one team became very excited and asked Nigel if they could torture the other teams!
(4) Non-planar graphs
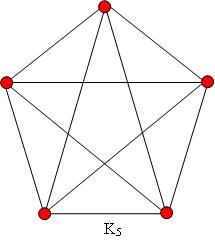
Nigel had students draw graphs on paper and discussed the concept of plane and planar graphs. As I recall he used a graph drawing program (it may have been Cabri Graph) that allowed topological reformation of graphs. A main topic of investigation was whether the complete graph on 5 vertices was planar, and if not, why not.
After much drawing, discussion and argumentation, the students came to he conclusion that  is not planar. Their arguments used the Jordan curve theorem implicitly. That is, they did not know, or articulate, the Jordan curve theorem, but from our perspective acted as if it were true.
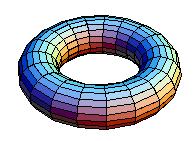
The next lesson Nigel and I got students making graphs on a torus, with the aim of them seeing that  can be drawn on a torus  so that edges meet only at the vertices. We gave them a choice of 3 models of a torus:
(a) A polystyrene solid torus, bought at a local craft store. Vertices were stick pins, and edges were long pipe cleaners.
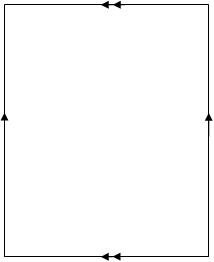
(b) Â A sheet of paper on which they could draw edges of the graph, with the usual edge identifications to make a torus:
(c) A computer-generated image of a torus in a Microsoft Word  document, on which they could draw vertices and edges, using a drawing program:
About half the class used physical models, a few students used the paper sheet with identifications, and the rest – almost half the class – used the computer image.
It turned out that a student whom Nigel, to that point, regarded as  one of the least mathematically able in the class, was the first to show that is a torus graph. He used the physical model.
So how did Nigel, who was not even Microsoft Word savvy, use technology in such a productive way to further his aims in creative mathematical exploration? Answer: he asked others for help, including students. If a student knew how to use Excel or Word to do something that Nigel did not, he would ask that student to explain to the rest of the class. Nigel never stood on ceremony. He was a partner in his students’ learning. He learned with them.
He was a wonderful teacher, a close friend, and I miss him so much that it hurts to write this. Â Ave atque vale, Nigel.
Are (mathematics) teaching and instruction synonomous?
Posted by: Gary Ernest Davis on: January 3, 2010
This post is a result of years of thinking about the question, pilule and a recent productive Twitter exchange with Peter Flom (statistician, advice educator, viagra thinker).
My answer to the question is: No, teaching and instruction have little to do with each other.
Let me try to explain this odd-sounding answer  by discussing a theory of teaching, which I will do in the context of teaching mathematics.
The term “theory” means that which is posited to be true, irrespective of how things might be  done, should be done, could be done. It is a posited account of what necessarily happens when teaching takes place.
Of course, this theory might be wrong – and probably is. Â But if it is provably wrong then we have learned more about the nature of teaching.
We cannot prove a theory is right, but we can hope that it is productive – that it suggests other things about teaching that might be true; that it gives us insights.
With that in mind, and with an awareness that  I will be shot down right away, because so many people just “know” that teaching is about instruction (a large number of them pre-service elementary teachers, in my experience) here goes.
A co-immunity theory of teaching mathematics
This is a theory of teaching based on a dual notion to the functioning of the human immune system.
I examine the idea that the major driving mechanism for a selectionist theory of teaching is extended chains of emotional interaction.
I will illustrate these ideas with an episode from one of our classes.
The punchline of this theory is that higher and more skilled symbolic development in mathematics is a result of  interactive emotional signaling between teacher and student.
The vertebrate immune system
Prior to the 1950’s it was widely thought that the human, and more generally vertebrate, immune system was instructed to produce antibodies by various noxious agents (antigens) from the environment outside the human body.
Two principal facts about the immune response lead to an entirely different theory of the immune system. These facts are:
(a) the immune system has a memory for a specific antigen. If an antigen gains entry to the body and stimulates the immune system, the next time this antigen does so the immune response is very substantially greater.
(b) The immune response is specific to a given antigen. If a different antigen gains entry to the body for the first time, the immune response to this antigen is more or less independent of its response to previous antigens.
To explain these facts Frank McFarlane Burnett & Peter Medawar (ref. Fix, 2004) developed the clonal selectionist theory of the immune response:
1. Human bodies contain numerous cells called lymphocytes and each
lymphocyte is responsive to a particular antigen by virtue of specific
surface receptor molecules.
2. Upon contacting its appropriate antigen, the lymphocyte is stimulated to proliferate (clonal expansion) and differentiate.
3. The expanded clone is responsible for the secondary response (more
cells to respond) while the differentiated (“effector”) cells secrete
antibody.
It is fair to say that this clonal selection theory of the vertebrate immune system, simply involving a different theoretical perspective than the instructional model, revolutionized immunology, and forms the theoretical basis of modern immunology with all its practical ramifications.
The human immune system (and that of all vertebra) serves the primary purpose of protecting the physical “self†from “non-self†– from the potentially harmful effects of the environment, ingested or admitted to the body through injury or other means. The very need to eat and breath raises the real possibility that animals will ingest or inhale harmful substances.
The theory of the immune system that prevailed prior to Burnett & Medawar was instructional: each antigen, so it was believed, provided a scheme of coded instructions for the invaded body to follow to produce antigens. Burnett & Medawar’s, independently developed, idea was that the body already contains a vast repertoire of antibodies and that an antigen selects the antibody that best fits its shape. In so doing, the antigen, by some means (as then unknown), stimulates the relevant antigen to clone itself.
The idea of co-immunity
Think now about teaching and learning mathematics. Here we have a situation in which a teacher expects to change the sense of self of a learner, to help the learner develop into a different person, with new skills a, new conceptions, and new insights. And the learner, from their side, expects to some degree to be changed, to learn, to be more than what one was at the beginning of a teaching episode, or teaching sequence.
This is sort of a dual, an opposite, of the function of the immune system. The immune system exists to preserve the physical self, but teaching episodes are designed to alter the mental self.
The immune system develops in the early years of life, from genetically given structures, to protect the developing physical self from harmful effects outside the self.
Teaching episodes serve to assist a learner to take on board productive, positive cultural aspects external to the learner. Just as a human needs to eat and breathe, and so potentially ingest or inhale noxious substances from which they are protected by a developing immune system, so a human needs to walk around and participate in the world, necessitating a long process of acquisition of external cultural ideas and practices.
Typically, a mathematics teacher designs an activity, presents an image, materials, or a suitable choice of text or problem, to a student. The teacher chooses these artifacts for the express purpose of bringing about a change in the thinking or skill set of a student.
Because of this dual role of teaching – bringing the cultural non-self to a learner for the express purpose of altering the learner – I regard (mathematics) teaching as having as its major role the development of co-immunity: the reverse of what the human (and vertebrate) immune system does in protecting self from harmful non-self influences.
Instruction or selection?
We have two clear choices in a co-immunity theory for how a teaching episode affects learning.
The first choice, an instructional model, is that by carrying out the activity, or by examining and engaging with the presented image, text, materials or problem, the student will be instructed, by some as yet unknown form of coded signal, to produce an altered brain state of more or less permanent character.
The second choice, a selectionist theory, is that by carrying out the activity, or by examining the presented materials, the student links the environmental signals from these artifacts to pre-existing neuronal structures. Furthermore, this linking stimulates a preferential linking for similar signals in the future. So far as learning is concerned this is more or less Hebbian learning theory (ref. Zull, 2002) . But so far as teaching is concerned it is a dramatically different theoretical point of view.
The aim of teaching is to alter and enlarge the student’s mental self, not to preserve it. In carrying out this aim a teacher does not act blindly: teaching artifacts are generally not presented randomly to students.
The selectionist perspective has been articulated by Zull (2002), in his attempts to conceive of teaching from a neuroscience perspective. He mentions, almost in passing, that when one thinks of the difficulty of building new neuronal connections in a progressively maturing brain, a selectionist view of how these new connections are formed seems most natural.
How might it work?
A theory without a proposed mechanism to produce results is hypothetical at best.
Darwin’s evolutionary theory of the origin of species (Darwin, 1859) gained enormous credence when the structure of DNA proposed by Watson & Crick (1953) suggested a mechanism by which genetic reproduction could take place. And this insight of Watson and Crick followed much prior work that indicated “genes†were real objects, not simply figments of the imagination.
What mechanism might account for a teacher’s ability to bring the outside mathematical culture to the inside mental milieu of a student?
Doubtless, if this theory has any credence at all, there will be manifold such mechanisms – nature generally utilizes as many diverse means as are necessary to get a job done. Yet one possible mechanism stands out, in my mind, as a leading contender as the driving engine of a co-immune theory of learning, and that is the utilization of extended chains of emotional signaling between teacher and students.
Greenspan & Stanley (2004) base a theory of symbol acquisition and
cognitive development on just this idea, which they term reciprocal, co-regulated emotional interaction.
The “co-regulated†nature of reciprocal emotional interactions is that together, teacher and student develop meanings for behaviors and responses, continually influencing one and other through reciprocal interactions of an emotional nature.
Greenspan & Stanley’s major argument is that this is how cognition and
symbol development take place – the fundamental basis of higher order symbolic cognition lies in its roots in emotional signaling , between child and care-giver, and student and teacher.
An example
A compelling example of how emotional signaling between teacher and student leads to higher level symbol formation, higher level cognitive processes, and the acquisition of external mathematical ideas, is presented in Davis & McGowen, 2004. I recount the main ideas here for purposes of illustration.
The situation described in that article is of a young woman, Blaine, who was enrolled, at the time, as a pre-service elementary teacher in a mathematics course. Following the sequence of teaching outlined in McGowen & Davis (2001) a number of combinatorial problems were given to the class. These included building block towers from a choice of two colors of blocks, walking up or right on an integer lattice, and expanding binomial expressions.
Previous experience with these problems had lead to sudden insights on the part of students as to the connections between these problems. In the class under discussion, no such insights had occurred at the end of the sequence of problems, so I decided to take a different tack and imagine that in walking up or right on an integer lattice, we did so if a tossed coin landed heads or tails respectively.
The class did this, tossing a number of coins and pooling results. Suddenly Blaine cried out loudly, and indicated, very emotionally, that she had seen something wonderful – that the coin tosses were distributing themselves according to a binomial distribution (not her words), and the proportion of differing numbers of heads and tails was obtained exactly from the integer lattice walking problem by dividing by an appropriate power of 2.
Blaine wrote a reflection, as the class did weekly, on her finding and on the strong emotional impact it had upon her. I congratulated her on the
power of her insight.
Several weeks later she was working with a group trying to figure out which pattern of black and whites was most common when 6 Othello pieces were scrambled and tipped randomly on a table. As she worked she disengaged from the task and began doodling something that resembled an integer lattice. I asked what she was doing, and she replied, rather off-handedly, that the problem reminded her of the integer lattice problem. I said that was good, and encouraged her to continue doing what she was doing.
As the class pooled their results they obtained an empirical result around 29% for 3 white and 3 black sides of Othello pieces. I asked Blaine if her method had yielded anything. She, deprecatingly, replied that she thought it was like the integer lattice problem, and that the answer therefore should be 20/64 which someone else calculated to be about 31.3%.
Blaine wrote about this episode in her next reflection and apologized for her poor memory in not recalling the answer immediately. I pointed out how her memory for the salient mathematical knowledge to recall was superb – absolutely correct – and that like all good mathematicians this schematic memory allowed her to reconstruct the details from a broad outline.
Blaine referred to the original episode of emotional recognition as a rush of connections, a glorious moment of clarity. The emotion in Blaine’s original insight was palpable. She and I discussed her feelings and what that insight meant to her. We discussed recalling those feelings and that insight in the course of another real-time problem. We discussed the genuinely powerful nature of her memory, guided by the emotion of her insight.
When Blaine wrote her final reflection for the course she expressed a deeply symbolic connection between all the combinatorial problems discussed in class. Her mathematical understanding was deep and deeply etched due, I argue, to the extended reciprocal nature of the emotional interchanges between us.
Is this new, or even useful?
Is there anything new in a co-immunity theory of teaching mathematics, coupled to a mechanism of reciprocal, co-regulated emotional interaction ? Or am I just restating some obvious well-known views on cultural transmission and affect in the learning and teaching of mathematics?
New or not, I think a co-immunity theory of teaching mathematics, focusing on selectionist principles, offers a simple yet powerfully focused way of thinking about how it is that external mathematical ideas become personal internally owned ideas.
Mathematics is a very symbolic subject so it is not surprising that something like Greenspan and Shankers’ notion of symbolic development through extended emotional signaling should play a significant role in cognitive mathematical development.
Doubtless, specific brain structures and functions – especially those connected to the emotions – play an absolutely essential role in understanding the details of a co-immunity theory of teaching.
Several substantial instructional theories have been tackled and largely replaced by selectionist theories since Darwin’s pioneering work on the origin of species. These are the instructional theories of speciation, the vertebrate immune system and the development in somatic time of the human brain (Edelman, 1987).
Teaching has survived, far too long in my view, as an instructional theory.
If the co-immunity theory of teaching tells us anything it is that teaching is largely not about instruction – it is rather based on a selectionist notion of brain development, with sustained reciprocal, co-regulated emotional signaling as its driving mechanism.
References
Darwin, C.: 1859, The Origin of Species by Means of Natural Selection, or The Preservation of Favoured Races in the Struggle for Life. London: John Murray.
Davis, G. E. & McGowen, M. A.: 2004, ‘A rush of connections, a glorious moment of clarity’. Networks, May. tortoise.oise.utoronto.ca/~networks
Edelman, G. M.: 1987, Neural Darwinism: The Theory of Neuronal Group Selection. NY: Basic Books.
Fix, D.F.: 2004, General Immunology. On-line at:
www.cehs.siu.edu/fix/medmicro/genimm.htm
Greenspan, S.I. & Shanker, S.G.: 2004, The First Idea. Cambridge, MA: De Capo Press.
McGowen, M.A. & Davis, G.E.: 2001, ‘Changing pre-service elementary teachers’ attitudes to algebra’. In H. Chick, K. Stacey, J. Vincent & J. Vincent (Eds.) Proceedings of the 12th ICMI Study on The Future of the Teaching and Learning of Algebra, vol. 2, pp.438-335. Melbourne, Australia: University of Melbourne.
Watson, J.D. & Crick, F.H.C.: 1953, ‘A structure for Deoxyribose Nucleic Acid’. Nature, vol. 171, 737.
Zull, J. E.: 2002, The Art of Changing the Brain: Enriching Teaching by Exploring the Biology of Learning. Virginia: Stylus.