When teaching prospective mathematics teachers at Rutgers University in New Jersey, I liked to shake up their preconceptions in mathematics, the unexamined assumptions that they had accepted as fact because they were told it was so.

So one evening I set the class the problem of finding how large they could make the sum of the angles of a triangle on a sphere.

For that purpose I had brought into class  several large oranges that I bought in a store in New Brunswick, a bunch of pins, some rubber bands, and protractors.

Students arranged themselves in groups to begin working on this problem.

One young man sat by himself and just stared at the orange in front of him.

When I asked what was the matter he said: “I don’t understand the problem.”

When I probed further he said that the angles of a triangle always added up to 180 degrees, so he couldn’t see what it was he had to do.

I told him to make a triangle anyway and measure the sum of the angles.

Another student, a young woman, said the task couldn’t be done because it is not possible to draw straight lines on a sphere.

When I asked the class what they thought about this, one student answered: ” You can draw them as straight as they can be on a sphere.”

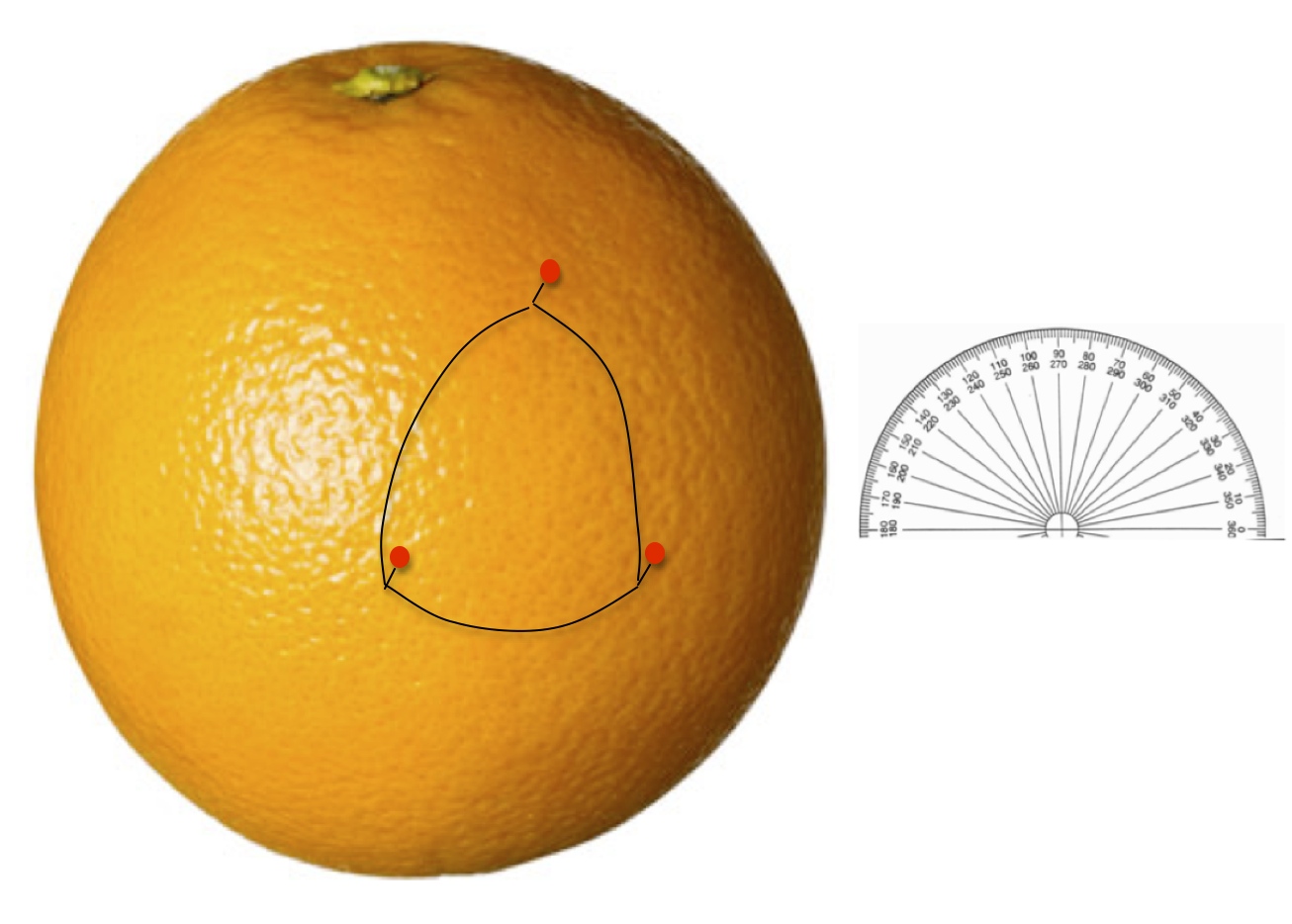
So after some discussion everyone set to making triangles on their oranges, with stick pins at the corners, and with rubber bands as sides.

They carefully measured the angles by pressing the protractor as flat as they could on the orange and taking a reading close to a stick pin.

After about 15 minutes the students reported that not once did the sum of the angles of triangles even look like 180 degrees.

One group reported that they could make the sum of the angles 270 degrees: start at the North pole of the orange – as if it were the Earth, travel straight down to the equator, go a quarter of the way around the orange and then back up to the North pole. Each angle was then 90 degrees, so the sum of the 3 angles was 270 degrees.

“What’s going on?” I asked them.

“Why isn’t the sum of the angles 180 degrees? Isn’t that what you learned in school?”

A student volunteered that it had to do with the oranges being curved.

Another student said that we weren’t actually measuring angles on the orange itself: it was, she  said, as if we had a sheet of paper that touched the orange at a corner of the triangle, and we were really measuring angles on that flat sheet of paper.

In reply, yet another student asked if that’s what we were doing – measuring angles on flat paper – then why didn’t the angles add to 180 degrees?

The student who raised the paper issue replied that the paper itself moved orientation from one corner of the triangle to another.

Yet another student asked why they hadn’t been taught this in school.

As as my habit I said: “That’s a very good question.”

A student volunteered: “Perhaps our teachers didn’t know.”

I asked what they would do with their own students.

To a person they said they would use this activity in their own class.

Mission accomplished?

Not quite!

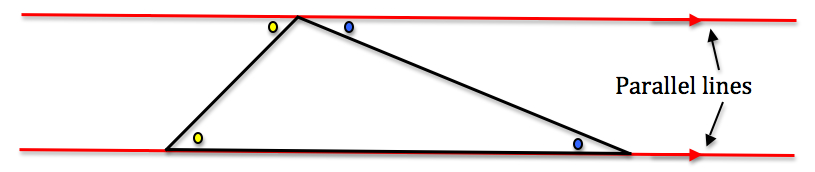
I asked them why the angles of a triangle on a flat surface (zero curvature) add to 180 degrees.

A couple of students volunteered tearing the corners of the  flat triangle on the paper, and re-arranging the corners to form a straight line angle of 180 degrees.

I asked them to do that on the orange, and, to their surprise, it didn’t work.

“So that’s no reason why“, I said.

I showed them the following diagram:

I asked them why his couldn’t be done on an orange.

It took a few minutes before someone said: “Because there are no parallel lines on an orange.”

Bingo!

About an hour and a half’s work, not counting buying oranges, and the scales over their eyes had dropped away.

Now they both knew that and why, through a lesson that was hard to forget.

Postscript

Dave Richeson (@divbyzero) asked: “Did anyone point out that the region outside the triangle is also a triangle, and its angle sum is even larger?”

The answer is no. I suspect that’s because the region “outside” the triangle didn’t look like a triangle to the students. The maximum angle sum they achieved was 3 right angles. Of course, even that was substantial progress.