I read a lot – particularly on #edchat and #edtech on Twitter – that “it’s about the pedagogy, not about the technology.”

There’s something about this that bugs me in relation to my current mathematical teaching and mathematical experience.

Maybe in language or English teaching the technology is “only a tool”. I want to argue a point of view that, for certain parts of mathematics the technology, the practice and the pedagogy cannot sensibly be separated.

Note I did say “sensibly”. We can, of course, always separate these things. The issue is whether it makes any real sense to do that.

So here’s a few things that come to mind from my recent experience where  the pedagogy does not come before the technology, where the technology is part and parcel of the pedagogy and the experience of doing  mathematics.

Graphs.

By this I mean nodes joined by edges:

When the graphs are small – not many nodes, not many edges – we can calculate quantities associated with them, and work out their relevant features, by hand.

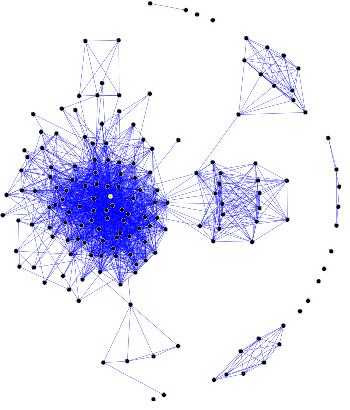
However, when the graphs get big, such as:

or:

Graph of internet traffic

we have no choice but to resort to technology to calculate and to discern deeper features- large and small scale – of such graphs.

This is not just a use of technology as a tool, for the reason that our object of inquiry – the graph itself- is presented to us as a computational object. It’s defining features- the nodes and their connecting edges – are given to us as lists in a database.  We can draw stunning pictures, such as those above, but the results are too complicated for our eyes and brain to comprehend at a deeper level.

Our very object of inquiry is a computational object, so using technology to explore it, to teach about it, to find its properties, is  both necessary and natural.

Statistics.

I am currently teaching a statistics course in which the first descriptive statistics exercise is to ascertain if there is a significant difference between he birth weights of smoking versus non-smoking mothers.

There are thousands of mothers in the data from the study. We could – with much patience and a lot of error – do the laborious calculations by hand. However, the data is presented to us as a computational object. It is a list of birth weights and smoking indicators. As such, the data naturally presents itself as something to be addressed through technological means.

Most students are using R, some Excel. Again, the technology is not “just a tool”, useful but not essential. Rather, the technology both educates and provides a natural point of engagement with the data.

The pedagogy, practice, and technology are not separate, nor sensibly or easily separable.

Differential equations

For the first 3 weeks students are working on modifications of Newton’s law of cooling and could do all calculations and drawings of graphs by hand. They do not, because I prefer to get them used to using professional grade tools such as MATLAB. That is a matter of choice, not of necessity.

In a couple of weeks time students will be tackling the numerical approximation of non-linear systems of differential equations. Here they need to carry out many thousands of difficult calculations, many times over. Once again, the object of inquiry is presented to us as a computational object, so learning about it and working with the technology are one and the same thing – not easily or sensibly separated.

Biological modeling

This class is working through a book on protein-protein interactions. The data about these interactions are specified in large data-bases. Again the objects of our inquiry are presented as computational objects, so learning about them is initially linked with the technology we use. The technology is a tool that is not easily or sensibly separated from the learning or the study of these objects.

_______________________________________________

You may say that this is all very well at the undergraduate level but in school we do not deal with such complicated mathematical objects.

With that statement I agree. However,  we can stick to mathematical issues or problems where there only small graphs, small data sets, simple differential equations, and we can avoid large chunks of biological data altogether. We can do that, but it’s not how much of the scientific, technological, engineering and business world is going these days.

Computational objects are becoming more and more common.

Twitter itself is a computational object. How many of us have never looked up our score on Twitter Grader?

For computationally presented  objects the use of technology to examine them, to learn about them, is essential.

It IS about the technology for these computational objects, and mathematics is rapidly developing an increasingly computational face.

Students whose mathematical learning is separate from the use of technology will be increasingly ill-equipped for the modern workplace.