Is commutativity of multiplication a natural concept?
Posted by: Gary Ernest Davis on: January 30, 2010
This post is a response to a tweet of Chiara Maieron, and a follow-up from Christopher Simpson.
The original tweet was:
“chiamai @republicofmath Heard kid who could multiply 4*9 but had troubles w 9*4 and wondered if commutativity concept is natural for math students ”
My initial response was that it depends on the kid’s concept of multiplication.
From a mature mathematical perspective, multiplication is essentially repeated addition  and can be defined inductively via 
However, Â for school children we do not define multiplication in this way. Â Most commonly, 
This is how many teachers would like student to think of multiplication, and it is then a nontrivial issue for a child, to appreciate that  m lots of n gives us the same quantity as n lots of m.
Geometrically, with some added color, it is clear this is so:
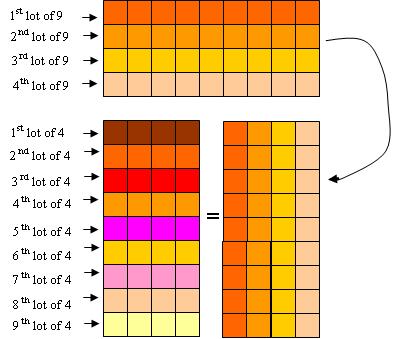When, for example, 4 lots of 9 is laid out with lots of 9 as rows, a transposition turns the rows into columns, so 4 columns of 9 rows becomes 9 rows of 4 columns. Â Whichever way we count the total we get 36.
But to a young child this might not be obvious until it is either experienced or pointed out.
A mature mathematician might “explain” the commutativity of multiplication by appeal to the inductive definition, and a teacher or child by appeal to transposition of a diagram, as above. Whatever, some level of justification or explanation is in order.
There is, it seems to me, nothing in the concept of multiplication that relieves us of the necessity to explain why it is a commutative operation.
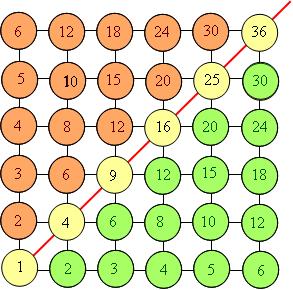
I have found that pre-service elementary teachers benefit from seeing multiplication filled in on the spots of (part of) an integer lattice:
For some reason, that is not quite clear to me, many pre-service elementary teachers find the symmetry of this diagram about the diagonal, shown, to be quite revealing. It is as if the geometric picture encapsulated in one fell swoop their vague, perhaps previously unspoken, understanding that multiplication is commutative.
Let Christopher Simpson and Chiara Maieron have the final words:
“TopherSimpson @republicofmath They always seem to get commutative and associative confused (no matter what I tell or show them). Maybe this will help”
“chiamai @republicofmath Thanks. I was curious because I grew up with the idea that commut. is “natural”, but then as a physicist I learned it is not.”
2 Responses to "Is commutativity of multiplication a natural concept?"
February 2, 2010 at 10:17 am
I have also presented it as follows:
3 x 4
= 4 + 4 + 4
Thinking of each of the fours above as 1 + 1 + 1 + 1, can I rearrange things so that instead of having three equal values added together, I have a sum of four (the other number in the original product) equal values? If I pull a one out of each 4 and dump it into a set of parentheses at the end, I get
= 3 + 3 + 3 + (1 + 1 + 1)
3 + 3 + 3 + 3 =
4 x 3
Which illustrates commutativity for one specific example. I usually leave it here, and suggest the student try this process for any two numbers of their choosing a few times to convince themselves that it will work for any two integers.
They will discover that if the two factors differ by more than one, they need to pull the difference between the two factors out of each repeated addition term, and create more than one new term at the end.
To show that this works for any two integers, if I have N x M, or N values of M added together, where N and M are arranged for convenience such that N < M:
N x M
= M + M + … + M
I will always be able to remove (M – N) ones from each M, turning it into
M – (M – N) = N
and placing all the ones in a set of parentheses at the end of the sum.
= N + N + … + N + (1 + 1 + … + 1)
= N X N + (1 + 1 + … + 1)
How many ones do I have in the pile at the end? N groups of (M – N) of them, or N x (M – N).
If I wish to show that N x M = M x N, I need to end up with M groups of N. I already have N of those groups (the Ns before the parentheses full of ones), so I just need to show that my pile of ones at the end can be turned into (M – N) groups of N or
N x (M – N)
But that is exactly the number of ones already in the pile. Therefore, this approach will work for any two integers N and M, and multiplication is most certainly commutative over the integers.
http://mathmaine.wordpress.org
Leave a Reply
January 31, 2010 at 10:40 am
Just a note of appreciation. I get so much out of all your posts, and the comments too.