Informal induction
Posted by: Gary Ernest Davis on: February 10, 2010
Th University of Massachusetts Dartmouth admits selected students, who do not qualify for regular university admission, into a special program with an extra foundation year.
Here’s the information from the University website:
“UMass Dartmouth offers two alternative admissions programs:
- College NOW
- START
They are intended for those who have completed high school or its equivalent, and who want to and can do university-level work, but whose academic achievements have been hampered by certain social, educational, or economic obstacles.
The university works with applicants to help them find the most appropriate avenue of admission either through regular admissions, or an alternative program such as College Now or START.”
Several semesters ago I was teaching a mathematics problem solving course in the START program. This course was devised by my late colleague Jim Kaput. The course has several aims including introducing students to  college level mathematics in an enjoyable way and increasing their problem solving skills.
Many of the students admitted to College NOW and START are first generation college students of Cape Verdean heritage. Â They have very deep and strong cultural and community ties, but are not especially attuned to an academic culture.
Apart from mathematics , English, and science, students in these programs take a course in study skills.
Among the many problems I set the class was the following:
Imagine a  square grid – same number of rows and columns – where the number of rows (and columns) is a power of 2: 2, 4, 8, 16, 32 ,…
Remove one corner square from that grid:
Is it always possible to tile the  grid with the corner removed by tiles of the following shape:
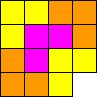
The class tried various combinations for a grid and, after a short time, found that they could tile a
grid, with corner removed, by L-shaped tiles:
The students struggled with an grid, until a young man, Mathias, declared he had the solution.
As is my custom, I asked him to go to the white board and share his solution with us.
Mathias was a confident, even brash, young man. He began to reconstruct his solution process on the white board, and become a little confused. The other students chimed in with suggestions, until Mathias quietened them, and carefully explained his basic idea:
Split the grid in half horizontally and vertically:
Remove corners from the full grids in the following way:
We know how to tile each of these grids with corners removed:
Put the grids back together again ,and put an L-shaped tile in the empty space in the middle:
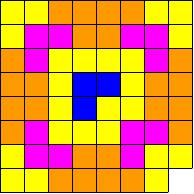 Mathias was very proud of his solution. He waved his hands to indicate the class could applaud, which they did. Mathias bowed and returned to his seat, beaming.
Mathias was very proud of his solution. He waved his hands to indicate the class could applaud, which they did. Mathias bowed and returned to his seat, beaming.
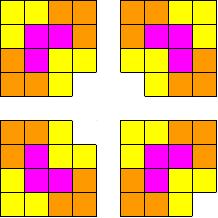
I asked Mathias and the class if they could now tile a grid with a corner removed. Mathias hesitated only slightly before saying that you would do the same thing – split the grid halfway horizontally and vertically  to get 4
grids, which we can tile, after we take away corners. So tile these grids, put them back together and put a single L-shaped tile in the middle.
When I asked why having a power of 2 number of rows and columns was important, a young woman in the class answered that it was because when you split a power of 2 in half, you still get a power of 2.
Mathias had essentially found for himself a  form of inductive construction – an informal inductive proof.
The inductive step is to split a grid in half horizontally and vertically, remove corners from the 3 full
grids, tile each of the smaller grids with corners removed, put them back together and add a single L-shaped tile in the middle empty space (where the corners were removed).
At the end of the class I asked Mathias what he had learned from his solution.
He asked “What I’ve learned?”
I repeated: “Yes. What have you learned from this?”
He thought for a moment, looked me in the eye, and said: ” What I’ve learned is that although we don’t know much, we’re not stupid.”
I think that sums up why we admit young people into these programs. Their  academic achievements have been hampered by certain social, educational, or economic obstacles, yet they want to learn and are capable of learning.
Further comments on induction
The solution to the tiling problem is a stronger statement than saying is  divisible by 3  for
.
This latter statement is often set as an exercise in induction, but, as my colleague Bob Speiser, an algebraic geometer, pointed out it’s a routine consequence of arithmetic modulo 3:
so Â
3 Responses to "Informal induction"
What a bright person. This was an example in a book I read so I never had a chance to try it myself, but I doubt it is so easy to spot.
As for the ‘further comment’ section: Even easier, 2^(2n) – 1 = (2^n-1)(2^n+1). Since 2^n is not a factor of three, one of the numbers left or right to it must be (as one is every three are). Hence shown.
Awesome post.Much thanks again. Fantastic.






February 10, 2010 at 9:23 am
Very nice!