Growth rates of simple integer recurrences
Posted by: Gary Ernest Davis on: June 5, 2012
The sequence of integers defined by
– where
, the floor of
, is the greatest integer
– begins 2, 3, 4, 6, 9, 13, 19, 28, 42, 63, 94, 141, 211, 316, 474, 711, 1066, 1599, 2398, 3597, 5395, 8092, 12138, 18207, 27310, 40965, 61447, 92170, 138255, 207382, 311073 and grows rapidly.
One can numerically estimate the growth rate of this sequence by first observing that the sequence of positive numbers is decreasing. This follows from the inequality
upon dividing by
, to get
.
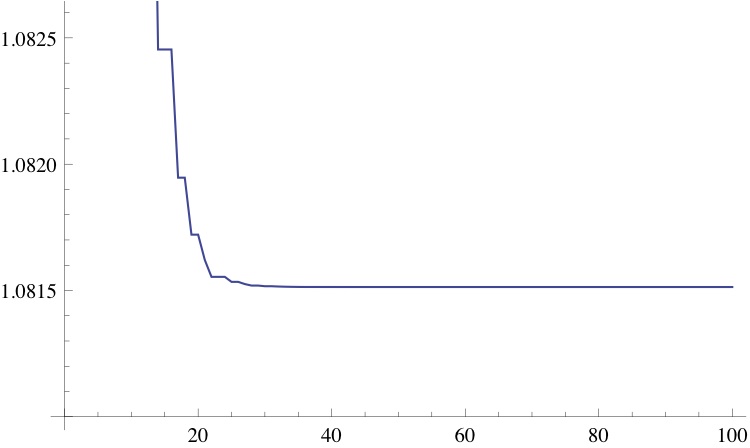
This means the sequence has a limit. In fact this sequence converges fairly rapidly to the limit:
| n | A(n)/(3/2)n | n | A(n)/(3/2)n | |
| 1 | 1.33333333333 | 34 | 1.08151439525 | |
| 2 | 1.33333333333 | 35 | 1.08151405187 | |
| 3 | 1.18518518519 | 36 | 1.08151382295 | |
| 4 | 1.18518518519 | 37 | 1.08151382295 | |
| 5 | 1.18518518519 | 38 | 1.08151382295 | |
| 6 | 1.14128943759 | 39 | 1.08151375512 | |
| 7 | 1.11202560585 | 40 | 1.08151375512 | |
| 8 | 1.09251638470 | 41 | 1.08151372497 | |
| 9 | 1.09251638470 | 42 | 1.08151370487 | |
| 10 | 1.09251638470 | 43 | 1.08151369148 | |
| 11 | 1.08673587473 | 44 | 1.08151368254 | |
| 12 | 1.08673587473 | 45 | 1.08151367659 | |
| 13 | 1.08416675918 | 46 | 1.08151367262 | |
| 14 | 1.08245401549 | 47 | 1.08151366997 | |
| 15 | 1.08245401549 | 48 | 1.08151366997 | |
| 16 | 1.08245401549 | 49 | 1.08151366880 | |
| 17 | 1.08194653587 | 50 | 1.08151366880 | |
| 18 | 1.08194653587 | 51 | 1.08151366880 | |
| 19 | 1.08172098938 | 52 | 1.08151366880 | |
| 20 | 1.08172098938 | 53 | 1.08151366880 | |
| 21 | 1.08162074649 | 54 | 1.08151366880 | |
| 22 | 1.08155391790 | 55 | 1.08151366869 | |
| 23 | 1.08155391790 | 56 | 1.08151366862 | |
| 24 | 1.08155391790 | 57 | 1.08151366862 | |
| 25 | 1.08153411684 | 58 | 1.08151366862 | |
| 26 | 1.08153411684 | 59 | 1.08151366860 | |
| 27 | 1.08152531636 | 60 | 1.08151366860 | |
| 28 | 1.08151944938 | 61 | 1.08151366859 | |
| 29 | 1.08151944938 | 62 | 1.08151366859 | |
| 30 | 1.08151684183 | 63 | 1.08151366859 | |
| 31 | 1.08151684183 | 64 | 1.08151366859 | |
| 32 | 1.08151568292 | 65 | 1.08151366859 | |
| 33 | 1.08151491032 | 66 | 1.08151366859 |
x
So we see that for large
.
What if we replace the constant 3/2 by a parameter ?
How does the sequence defined by
grow?
As before we see there is a constant such that
An obvious question is: how does ?
A moment’s thought shows that the answer is only interesting for
The following Mathematica® code computes to a decent approximation:
A[1, r_] = 2;
A[n_, r_] := A[n, r] = Floor[r*A[n – 1, r]];
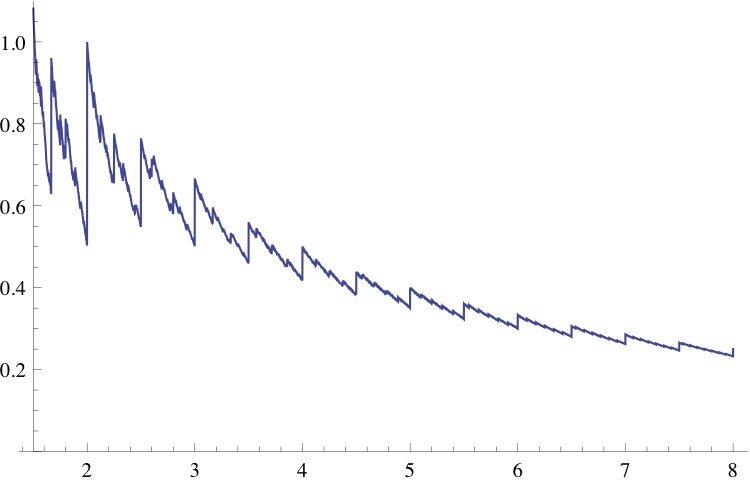
T = Table[{r, Table[N[A[n, r]/r^n], {n, 1, 100}][[-1]]}, {r, 1.5, 5, 0.001}];
ListPlot[T, Joined -> True]
and the resulting plot of looks as follows:
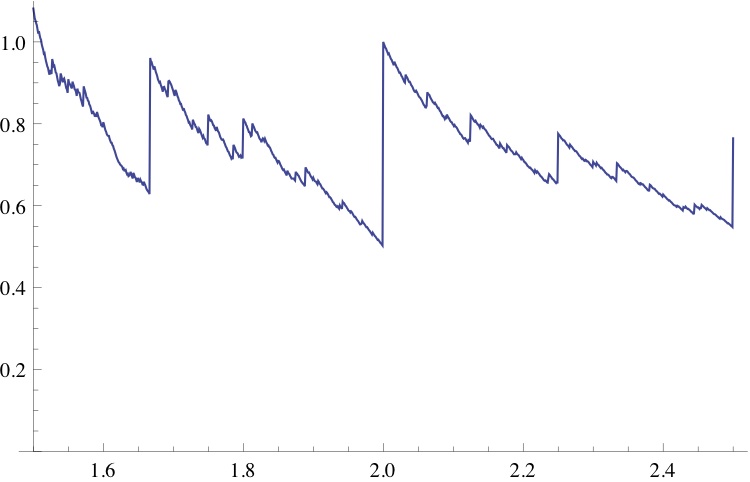
A blow-up of the portion of the plot for looks as follows:

June 8, 2012 at 12:08 pm
Some questions that came to my mind as I read this:
1. Is K(r) rational or irrational? Algebraic or transcendental?
2. How does the initial value of the sequence change the behavior of the sequence?
Something for me to play around with in my spare time. Thanks!