Computational media: the universal acid of mathematics teaching (1)
Posted by: Gary Ernest Davis on: December 17, 2009
The times they are a-changing
In Darwin’s Dangerous Idea, Daniel Dennett discusses a fantasy universal acid that eats through and transforms  all containers into which it is placed. He applies this notion of universal transformation to Darwin’s evolutionary theory, and writes:
“… it eats through just about every traditional concept, and leaves in its wake a revolutionized world-view, with most of the old landmarks still recognizable, but transformed in fundamental ways.â€
I claim that digital technology, particularly in the form of computational media,  is a universal acid to the practice of teaching mathematics. We are, I contend, going through a process of re-thinking education, particularly in relation to mathematics and science, more profound than at any other time in human history. Old  topics and skills that seemed so critical just a few years ago are now  being brought into question. The nature of mathematical skill and cognition is under a spotlight, and many teachers at all levels, K-20, are becoming confused and concerned about the changes afoot.  I see in my colleagues, both in universities and schools, aspects of Kübler-Ross’s 5 stages of grief: denial, anger, bargaining, depression and acceptance. There is no holding the universal acid of computational media, so far as mathematics is concerned. All previous ways of acting and behaving, all esteemed skills, are being radically transformed as computational media eats away at  practices of mathematical education. Many teachers are in denial, many are angry, quite a few are depressed, and relatively few, yet, are accepting of the changes being wrought by the universal acid of computational media.
Computational media
Maple
I currently teach calculus and differential equations to science, engineering and mathematics majors. Fall semester 2009 I had a class of 44 engineering students, 40 young men and 4 young women, for multi-variable calculus. Anyone who knows anything about this subject will know it is very geometric in nature, with the behavior of vector fields in 2 and 3 dimensions on center stage.
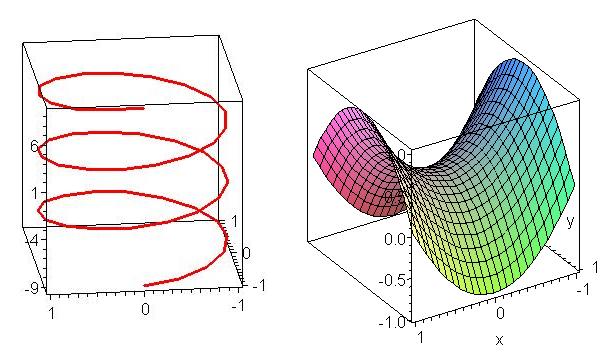
Students, who are typically 19-20 years old, complain that they have trouble drawing 3-dimensional pictures. I tell them we all do (some geniuses excepted). The engineering computer lab in which the class is held is equipped with one computer for every two students. Those computers have up-to-date versions of Maple installed. Â The engineering faculty expect that Maple will be used in one way or another to enhance student understanding of calculus concepts. One way Maple can do that is by plotting curves and surfaces that student find hard to do, such as a helix or a saddle:
Maple is not perfect at this job: using an inappropriate coordinate system can result in an unrecognizable picture. For example, here’s how Maple draws the cone using default rectangular coordinates :
Maple acts nicely to help students see more clearly in 3 dimensions, and to assist them in drawing better pictures, as a result of their clearer 3-dimensional  vision. This is a very positive aspect of computational media – of which Maple is an excellent example – and most mathematics teachers are keen to use this sort of technology for the purpose of assisting students to develop skills of thinking in 3 dimensions.
The same students generally do not recall facts and procedures from earlier calculus classes and still have quite weak algebraic skills. Very few can recall how to solve a quadratic equation, their trigonometric skills are weak, and they make a lot of algebraic mistakes.  If these students have to integrate by parts or by substitution they generally do not recall well how to do that. So  when it comes to double and triple integrals, and line integrals, these students are generally lost, way at sea.
I can, and do, get them practicing examples. Yet when they are bogged down with an algebraic expression, or with a simple single integral that they have forgotten how to do, I get them to do it with Maple. “Just let Maple do it” I say. “It knows how to better than you.”
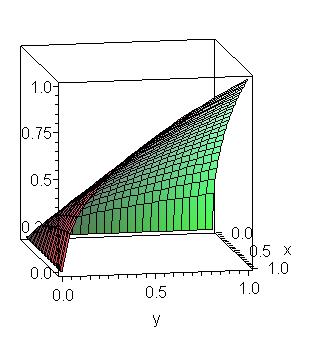
Maple does the algebra
Maple calculates an integral
Is this bad of me? Shouldn’t they be learning these skills? Well, here’s where computational media as universal acid comes in: Maple can do all the algebra and all the integrals the students might ever be able to do, quicker and more accurately than they ever will. So what skills, what ways of thinking, what habits of mind, what learning outcomes do I really want? What does anyone want, and why?
The universal acid of computational media is eating away at and transforming the actual or likely skills base of these engineering students. After all, when they are engineers in a lab, workshop, or the field, do you seriously imagine they will work out a triple integral in their heads or by hand? No, of course not. They will use the software available on their workstation, netbook or cell phone. Yes: cell phone. Mathematics apps for cell phones can already do such complicated mathematical calculations, and draw relevant 3-dimensional pictures. Â There is a drawback: currently these are expensive cell phone apps. They cost, oh, all of $30. You got it – $30 for an app that might previously have cost a thousand dollars, even if it were available for a cell phone at such an elevated price.
So you can see how computational media eats away at our conception of  important mathematical skills for engineers. Until a few years ago it was – rightly – regarded as very important that engineers should know how to work out complicated  integrals by hand. But now computational media can do better than them, more accurately, in a twinkling of an eye. Do farmers still plow their fields with oxen? Not if they are smart. Why then, should engineers calculate hard integrals, which they will likely get wrong if they are out of practice, by hand?
We can,  if we wish, be in denial, and refuse to engage with the question. The continuing and rapid improvement in computational media, and its widespread availability, mean that  if we are in denial, we will soon be angry!
MATLAB
Fall 2009 I also taught a beginning course in differential equations, as I have done for several semesters now. Students in this class are largely engineers and mathematics majors. I use MATLAB as a computational engine for this course, not because I like it (I loathe its command-line interface) but because it is industry standard for engineers and computational scientists.
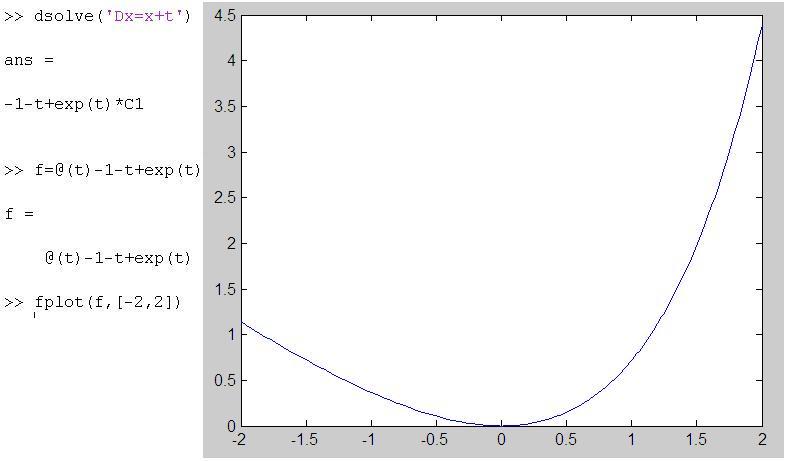
MATLAB has in-built procedures and functions for solving differential equations – either exactly or via numerical approximations when exact solutions are not possible.  Existing differential equations texts, even those using MATLAB as a computational engine, spend most of the chapters on different methods for solving differential equations. There are two relevant facts to bear in mind here. First most differential equations do not have exact solutions, and we have to resort to numerical approximation. This is most likely to be true of differential equations engineers will encounter in their working lives. Secondly, MATLAB can solve  differential equations that have an exact solution. It does this at the press of  a key, and will, if asked nicely, plot a graph of the solution.
Should I be teaching these students how to solve differential equations using pencil and paper? Or should I be teaching them to  use MATLAB and to discuss the features of the solution – its formula and its plot – as something they might or might not have expected from the differential equation. Should I, in other words, be building their intuition and sense of meaning for solutions of differential equations, and leaving the – fairly messy – grunt work to MATLAB?
Once again, the universal acid of computational media confronts us with this question. We can be in denial and we can, before long, be angry and then depressed. Sooner or later we will have to accept that computational media is transforming what we teach and how we teach mathematics. Â Today’s important skills may be consigned to tomorrow’s trash can.
Geometer’s Sketchpad and Cabri
Geometer’s Sketchpad (GSP) and Cabri are most often thought of as dynamic geometry environments. From a geometry perspective the computational media aspect of these software is the ability to dynamically instantiate relationships between differing aspects of a geometric figure. One moves around a figure and certain features of the figure – relationships between certain lines, circle and points – remains constant.
GSP and Cabri have been been widely in schools as valuable  computational media that strengthens students geometric understanding. Somewhat less well  known or utilized is how much computational mathematics can be carried out in these environments: Key Curriculum Press has a free booklet with examples of the use of GSP in a number of mathematical areas.
GSP had, in the past, been dismissed by some college and university faculty as a mere toy, despite Jean-Marie Laborde having based Cabri, on which GSP is based, on his earlier program Cabri Graph, which was a software tool for professional mathematicians. Despite these earlier grumblings (anger?) some colleges are now using GSP in undergraduate courses, including statistics and geometry.
GSP and Cabri have been success stories in computational media in that they have helped revive and reinvigorate the teaching of geometry, as well as providing a platform for exploring and learning about many aspects of mathematics.
This aspect of the universal acid of computational media has not effected a complete transformation yet: I know of a number of teachers of mathematics who are opposed to spending the time to learn how to use GSP in their classrooms for what they perceive to be minimal  benefits (denial?)
Wolfram Alpha
With Wolfram Alpha we get right to the heart of the transformative effect of the universal acid of computational media, and the anger and denial expressed by many school teachers at how students use this medium.
Stephen Wolfram , inventor of Mathematica, and computational scientist, has envisioned Wolfram Alpha as a gigantic computational engine that, as it is asked computational questions, learns answers and how to do more extensive and deep calculations.
How does this impact middle and high school students and their teachers, who are unlikely to ask deep computational questions? Well, Wolfram Alpha will do homework for kids. Now you see the problem. Imagine a teacher sets some questions on solution of quadratic equations as homework. Following a non-computational media mind-set the teacher is most likely thinking that students will learn about the mechanics and procedures of solving quadratic equations by attempting the homework problems. Instead, these very 21st century students ask Wolfram Alpha to do their homework.
But wouldn’t the teacher be able to spot something fishy, because the students would  have an answer but no working,  the grunt work being done by Wolfram Alpha? Well maybe not, because Wolfram Alpha will show the steps in solving quadratic equations.  So students can put the question to Wolfram Alpha, which obliges with an answer showing all working. Students can copy this answer in their own hand to show the teacher. Currently Wolfram Alpha does this by completing the square. So if the teacher expected a routine use of the quadratic formula, or spotting factors, then the student would still have a  little bit of work to do (bit not much).
No surprise that this makes a lot of teachers angry: the computational media undermines the very skills the teachers wanted their students to practice. Could teachers think about why they wanted students to have these skills in the first place? Just because that’s the way it’s done doesn’t mean that’s how it was always done, or will always be done. The computational media is putting the question to us or, rather, putting us to the question.
I discussed this issue with university colleagues who are of the opinion that solving quadratic equations by hand is a valuable and necessary skill because it is used a lot in calculus. Well carving letters in rocks was a necessary and valued skill before paper was invented, yet only  a very few people know how to carve letters into marble now.
You see my point? Â Computational media is forcing us, like it or not, to think about what mathematical skills we value and why. There’s no escaping it. So, if you are troubled … go away and deny it’s happening for a while, at least until you get really angry, and then we can move on to bargaining.
Be careful out there – it’s  a rapidly changing world, as Bob Dylan so poignantly noted.
6 Responses to "Computational media: the universal acid of mathematics teaching (1)"
I couldn’t agree with you more, Taleese! If only more math teachers k-6 had a similar outlook, we might not have as many math issues when students encounter Algebra!
Keep up the great Work!
[…] like to respond to a blog post about how new computational media (MAPLE, MATLAB, Wolfram|Alpha, GeoGebra, Cabri, etc…), […]
This is an interesting and important issue. We all need to do some hard thinking about the goals of math education in the computer age. I agree that computational fluency cannot be the main objective, since computers can calculate more quickly and accurately than any human. Conceptual understanding is closer to the mark, but how do we assess understanding?
In my opinion, the principle objective is that students should be able to reason mathematically, and support their conclusions with clear, correct, and convincing arguments. These arguments may be produced using manual calculation, computer calculation, or a combination. Learning to do simple calculations by hand is the first step in learning to produce mathematical arguments, but it is not the primary purpose.
I agree with Taleese that students must possess mathematical knowledge in order to use a calculator effectively. Training people to press calculator buttons is not math education. But I do not agree that a calculator is merely a time-saver. Trigonometry students should know how to solve triangles, but there is no need for them to know how to evaluate the trigonometric functions by hand. Geometry students should be able to apply the Pythagorean theorem, but do not need to know how to calculate square roots by hand. Statistics students need not know how to evaluate the Gauss error function. It makes no sense to defer teaching important mathematical concepts until their computational skills catch up.
Of course, in many real world applications, it is simply not possible for a human to calculate a solution by hand. Systems of equations with thousands of variables cannot be solved without technological assistance.
The problem is that since they didn’t learn the paper and pencil versions, they don’t really get what is going on. Therefore if they fat finger the calculations or somehow mess up the input or computational instructions, they won’t recognize they have an error. Furthermore, how can we ever hope that students will find the beauty in mathematics if they are only pushing buttons? The argument of your colleagues shouldn’t be “well they need to learn it because we use it later” it should be “they need to learn it because it strenghthens their brains and gives them a sense of the beauty of math.” I go to the gym to make my body better and stronger. We have machines to lift things, though. But a strong body is a healthy body. We do paper and pencil integrals because a strong mind is a healthy mind. Having a machine do all the work is fine in day to day life, but the brain has to get to the gym too. That’s what college classes are – Bally’s for the brain.
@Bonster713
I don’t think the classical approach of repeated drill and practice is doing a very good job of encouraging students to discover the “beauty of math”. If the use of computational media allows the instructor to introduce more interesting problems, as described in the article, then I’m largely in favor of it. The article doesn’t suggest that pen-and-paper math be eliminated, but rather proposes that the goals of math education go beyond just computation. There IS more to math than just computation and Kurt Gödel’s Incompleteness Theorem is proof of it. Alan Turing extended this result to show that certain problems are simply not computable. Between these two results, the effort to turn one’s brain into a computer through repeated practice seems self-defeating. I think its important to find a balance in math education between using technology to solve problems and understanding how that technology works. Students need to learn to think critically about problems in math and not just blindly follow a prescribed procedure.

December 17, 2009 at 7:01 pm
In sixth grade, the differences of opinion I most hear about involve calculators. But here’s the thing-so it’s faster. That’s all a calculator should be-faster. Never “smarter”. The person operating the calculator should first possess the knowledge, know-how!, and ability through practice to know how to compute an answer for themselves. In other words, a calculator and any other technology should never substitute for a brain.
Remember, with all technology whatever the format, it must be programmed to do the work, by a person. We need people who know how and who can.
I have a mentally retarded son (9). He’s allowed to use a calculator in school, but I don’t let him use one for his homework-because he doesn’t get IT yet. I want him to know math, understand math, and do-practice math, more than I want him to complete math. (Can’t a monkey be trained to press a button?)
Plus, as a teacher-I’m at the point, where I believe I’ll give my students all of the answers in advance (I’ve begun on occasion, and my daughter’s math teacher already does 100% of the time.) I don’t really care about the answer-I care about the path to the answer.