My wife likes to eat at Not Your Average Joe’s on Route 6 in Dartmouth, Massachusetss. I’m a vegetarian so my choices are more lmited. NYAJ has passable choices for a vegetarian, inlcuding pizzas. Usually a 10″ garden pizza does me.

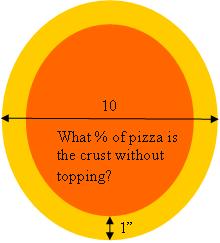
When I first started ordering pizzas from Joe’s I was still teaching pre-service elementary teachers mathematics, so when I noticed that Joe’s leaves a full 1″ of pizza crust without any sauce or topping I thought: what a good exercise to get my students to figure out the percentage of pizza without topping.

In my experience most people don’t think to quantify their experiences this way. I think they should – it can be an eye-opener. If you doubt me, think about the price of toner-cartridge ink in dollars per gallon.  This is what quantitative literacy is about.

Here’s a picture of pizzas from Joe’s on-line menu:

and here’s a diagram of what I was looking for:

Not all pre-service elementary teachers recall how to calculate the area of a circular region, but in a class of 25 or so usually someone does.

So, someone in the class calculates that the area of the whole pizza is   square inches.

At this point some students want to repace  by to get an area of approximately 78.6 square inches.

Surprisingly, to me, some students do not approximate . It seems almost as if they can see that the occurrences of will cancel as they calculate the percentage of the pizza without topping.

They next calculate that the area of pizza with topping  is square inches, so the area of pizza without topping is square inches.

The ratio of the area of pizza without topping to the area of the pizza is .

So 36% of the pizza has no topping. Wow! That’s over of the entire pizza! Shouldn’t Joe’s lower their  prices?

This result is almost always an eye-opener to pre-service elementary teachers. They find it hard to believe that so much of the area of the pizza lies around the edge.

Usually I ask them to calculate the percentage of pizza without topping if they don’t know the diameter, but know that 1″ of the crust has no topping. This level of algebraic thinking usually stumps them.

When the class is happy with their answer I ask them how they know that the area of a circular region with diameter is , or, in other words, that the area of a circular region of radius   is .

Invariably it’s just a formula they remember, if they did in fact remember it. Those who didn’t remember it usually agree that it sounds right.

When I ask them what is , I either get an answer of or something like: “It’s the circumference; it’s like, the circumference is times the radius.”

So what some of them seem to know about is that  a circle of radius has a circumference of .

Building on that, I draw a pizza of radius with many more slices than usual:

I then take those slices and arrange them side by side, alternately one up, one down:

With very thin slices the rearranged pizza is looking very much like a rectangle, with width approximately half the circumference  of the circle, and height approximately the radius of the circle:

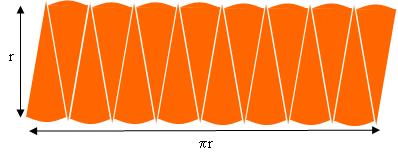So with very thin slices the area of the rearranged pizza is approximately .

This is an approximation, but as the pizza slices are made thinner and thinner it is a better and better approximation.

_______________________________________________

The strange fact of a large proportion of the area of a circular region lying close to the perimeter is related to the annoying phenomenon of looking for a place in a road map and finding it near the edge of the page, so having to go to the next page for a complete picture.

Of course this recollection is getting pretty old-fashioned as GPS replaces paper maps. But for those of us who recall it, here’s what happens:

Let’s suppose the maps are drawn on US letter, , and that we are annoyed if the place we want is within ” of the edge of the page.  How often are we likely to be annoyed?

The area of the page is 93.5 square inches, and the area of the region within ” of the margin is square inches.

Supposing the place we want is more or less randomly distributed on the page we will be annoyed  % of the time – about 1 time in 5.