Ï€ does go on forever (unpredictably)
Posted by: Gary Ernest Davis on: January 26, 2011

Reuters new agency reported on January 20, here 2011 that a Japanese systems engineer, Shigeru Kondo, had used a home-built computer to calculate to trillions of digits and thereby broken the existing Guinness Book of Records entry for calculating
.
A sentence toward the end of the report caught my eye:
“Calculating a more accurate pi, which is believed to go on forever, has been a challenge for scholars for thousands of years, ever since the parameter was used in ancient Egypt.” (My emphasis)
 is not a rational number
is not a rational number
Of course the decimal expansion of goes on forever, because
is not a rational number. That is, there are no integers
for which
.
This was first proved by Johann Heinrich Lambert in 1761.
The irrationality of means not only does the decimal expansion of
go on forever, but that it never repeats from some point on.
Of course we are familiar with rational numbers whose decimal expansions repeat, such as ,
and
which repeats after the first two decimal places.
Equally, any decimal that eventually repeats is a rational number.
The reason for this is fairly straightforward.
First, if is a number that has a repeating decimal after, say, the
decimal place then
is a repeating decimal.
Second, repeating decimals are rational numbers – just multiply
by
where
is the length of the repeating block, to get
.
For example, if then
and if
then
so
. So
is a rational number, and so therefore is
.
All this means that not only does the decimal expansion of go on forever, it never eventually repeats.
 is transcendental
is transcendental
The same is true, of course, for which is an irrational number.
What distinguishes from a number such as
is that the latter is algebraic.
A number is “algebraic” if there is a polynomial
all of whose coefficients are integers, for which
Of course, in the case of such a polynomial is
.
For there is no such polynomial. This is what is means for
to be a transcendental number:
is not algebraic.
This was first proved by Ferdinand von Lindemann in 1882.
Algebraic numbers are in many respects easier to understand than non-algebraic (= transcendental ) numbers. In fact, Leopold Kronecker denied the existence of transcendental numbers (including ).
Are the digits of  random?
random?
This is a very difficult question to answer unless we have a workable definition of “random”.
Gregory Chaitin and Andrey Nikolaevich Kolmogorov came up with a definition of “algorithmic randomness” which has to do with the non-compressibility of the description of a number. While this is an interesting and useful idea it does not seem to correspond exactly to what most people think of as randomness.
In practice, a sequence of numbers – such as the digits of – is NOT random if it fails one of a batch of tests for randomness.
What this means in practice is that we cannot prove that a sequence of numbers is random, only that it is not random.
If a sequence of numbers passes all known tests for randomness we tentatively conclude that the sequence is behaving like a random sequence.
A 2001 research report by Paul Preuss at Berkley, indicates that the sequence of digits of does behave as if it were random.
So not only, do the digits of go on forever, they do not eventually repeat, and appear to all intents and purposes, to be random.
6 Responses to "Ï€ does go on forever (unpredictably)"
[…] This post was mentioned on Twitter by Tito Eliatron, MiGUi and Juan Malagon, Republic of Math. Republic of Math said: Ï€ does go on forever (unpredictably) #pi #math http://wp.me/pJESd-18b […]
If x = 0.2135656565656…, then 1000 * x = 213 + 0.56565656…
Thanks! Fixed.
About pi
An informative reading on interesting facts about . We will indeed try to estimate its value later in SYE 6005.

January 26, 2011 at 1:29 pm
I enjoy asking my students this question –
True or False: since the digits of pi ‘go on forever’, pi has no definite location on the number line.
Many students consider that a true statement. “How can pi have a definite location if it ‘never ends’?” they ask. I ask them, “So you think it creates a smudge on the number line?” They’re not sure. It’s a very interesting discussion to have, and I think very important. I see how they can form an idea like that from how we use our terms. I try to make it clear to them in the course of discussion that pi does in fact have a specific value and a specific location on the number line – it is the decimal REPRESENTATION that ‘goes on forever’.
– Michel
January 26, 2011 at 2:29 pm
Michel,
I did wonder about writing on this. You are absolutely right.
A question is what people think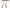 is: is it the decimal representation (if so, we only know so much about it, and may never know everything); is it the area of a unit circle? If so, what tells us a unit circle has an area? We can of course use inner and outer measures and limits to show that a circle HAS an area, and that area is called
is: is it the decimal representation (if so, we only know so much about it, and may never know everything); is it the area of a unit circle? If so, what tells us a unit circle has an area? We can of course use inner and outer measures and limits to show that a circle HAS an area, and that area is called 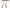 , but that’s a bit sophisticated for beginners.
, but that’s a bit sophisticated for beginners.
There are many other ways to approach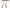 . For example, as the first positive number
. For example, as the first positive number  for which
for which  .
.
Whatever approach we use,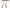 comes out as a real number.
comes out as a real number.
Of course, Kronecker did not agree.