"See, that’s the sickness right there. You find math fun, don’t you?"
Posted by: Gary Ernest Davis on: September 27, 2010
The title of this post comes from an interview with “Punk Mathematics” author Tom Henderson.
There are lots of websites with the words “Fun” and “Math” in their title. But many of these sites are just clowning around to be funny without making the math itself fun.
Bubblz
Bubblz is a math clown with a difference.
There’s no doubt that Bubblz is a clown. Yet, it seems to me that Bubblz is funny, entertaining, educates, and makes the math humorous too.
Martin Gardner: The man who made mathematics fun
Martin Gardner, who died this year, was a prolific writer on mathematics and science.
He seemed to induce people to think that mathematics is fun:
Inigo Montoya wrote, May 23, 2010:
Go well, Mr Gardner. For me, you made mathematics real. You made it fun. I can’t thank you enough.
MikeMoore wrote, 7:20 PM Saturday, May 22, 2010:
RIP Mr. Gardner…you introduced me to the world of math & science, and taught me it could be fun too! Without you I would have never considered studying mathematics, computer science, or linguistics…
Thank you!
Anon wrote, 7:59 AM Sunday, May 23, 2010:
RIP Master Methemagician Gardner. Thank you for allowing my students to discover the magically fun side of math!
Scientific American profile of Martin Gardner
A mathematician plays and has fun
Paul Lockhart, writes in “A Mathematician’s Lament“:
” …if I’m in the mood to think about shapes— and I often am— I might imagine a triangle inside a rectangular box:
I wonder how much of the box the triangle takes up? Two-thirds maybe? The important thing to understand is that I’m not talking about this drawing of a triangle in a box. Nor am I talking about some metal triangle forming part of a girder system for a bridge. There’s no ulterior practical purpose here. I’m just playing. That’s what math is— wondering, playing, amusing yourself with your imagination. For one thing, the question of how much of the box the triangle takes up doesn’t even make any sense for real, physical objects. Even the most carefully made physical triangle is still a hopelessly complicated collection of jiggling atoms; it changes its size from one minute to the next. That is, unless you want to talk about some sort of approximate measurements. Well, that’s where the aesthetic comes in. That’s just not simple, and consequently it is an ugly question which depends on all sorts of real-world details. Let’s leave that to the scientists. The mathematical question is about an imaginary triangle inside an imaginary box. The edges are perfect because I want them to be— that is the sort of object I prefer to think about. This is a major theme in mathematics: things are what you want them to be. You have endless choices; there is no reality to get in your way.
On the other hand, once you have made your choices (for example I might choose to make my triangle symmetrical, or not) then your new creations do what they do, whether you like it or not. This is the amazing thing about making imaginary patterns: they talk back! The triangle takes up a certain amount of its box, and I don’t have any control over what that amount is.
There is a number out there, maybe it’s two-thirds, maybe it isn’t, but I don’t get to say what it is. I have to find out what it is.
So we get to play and imagine whatever we want and make patterns and ask questions about them. But how do we answer these questions? It’s not at all like science. There’s no experiment I can do with test tubes and equipment and whatnot that will tell me the truth about a figment of my imagination. The only way to get at the truth about our imaginations is to use our imaginations, and that is hard work. In the case of the triangle in its box, I do see something simple and pretty:
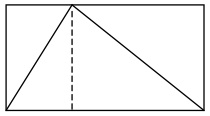
If I chop the rectangle into two pieces like this, I can see that each piece is cut diagonally in half by the sides of the triangle. So there is just as much space inside the triangle as outside. That means that the triangle must take up exactly half the box!
This is what a piece of mathematics looks and feels like. That little narrative is an example of the mathematician’s art: asking simple and elegant questions about our imaginary creations, and crafting satisfying and beautiful explanations. There is really nothing else quite like this realm of pure idea; it’s fascinating, it’s fun, and it’s free!”
Fun with problem solving
Several years ago I gave the following problem to a group of students enrolled in a pre-engineering course. A couple of them were adamant it was impossible to solve because the information given was not relevant to the solution. They persisted for about a half hour and when they got the answer there was much hilarity and incredulity that they could actually figure out an answer.
One day two people Erik and Deborah, meet in the street.
“Hello Erik, it’s been a while since I’ve seen you. How old are your 3 boys now?” asks Deborah.
Erik, knowing Deborah is a mathematician, poses a puzzle for her:
“When I multiply their ages I get 36.”
Rising to the challenge, Deborah sad she needed more information than that to work out their ages.
Erik pointed to a nearby house and said:Â “When I add their ages I get a number equal to the number of windows in that building.”
Deborah thought for a second, and said she still needed more information.
“OK”, said Erik, “my eldest boy has blue eyes.”
“Got it!” said Deborah, laughing.
How did Deborah work out the boys ages ?
Be careful! You might have fun!
3 Responses to ""See, that’s the sickness right there. You find math fun, don’t you?""
I don’t get it. I can see we need 3 natural numbers that multiplied make 36 and of which one is greater than the other two. But that doesn’t still give us the possibilities of 9,2,2 and 6,3,2 and 4,3,3 ? Actually, what does the last hint mean? If he mentioned the yougest one, I could say that only one possibilty _has_ a youngest, but that one is eldest is redundant and I can’t see what other relevant information we are being given o.o
I hope you can help me;
puzzled handshake;
Lobz




September 28, 2010 at 10:51 pm
Since which assumptions are possible or not possible, I only saw fit to use the first piece of information. There are only three factorizations using three factors each:
4, 3, 3; 3, 6, 2; and 2, 2, 9.
Likely the duplicated factors in each factorization are not reasonable unless we accept outside facts of twins, or adoptions. This seems to allow then only one set of ages: the 2, 3, 6.
We might also expect that the age-two child was not quite born or was just newly born “two years ago”, when Erik and Deborah last met.
Just tell me if I missed something important. Based on the description, we cannot SEE the “number of windows in that building.”
September 29, 2010 at 5:28 am
I was not thinking when I wrote “a couple of years”. I should have written, as I now have, “it’s been a while since I’ve seen you.”