The value of cos(pi/5)
Posted by: Gary Ernest Davis on: December 3, 2010
@capedsam Tweeted: “Can you find an exact value for cos(pi/5)? “

x
It is actually fairly easy to find an exact value for  by following a path through the complex numbers.
by following a path through the complex numbers.
x
To do this we use Euler’s identity  for all real numbers
for all real numbers  .
.
x
Jim Tanton (@jamestanton) has a very nice introduction to Euler’s identity here.
x
As shorthand let’s write 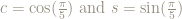 .
.
x
From Euler’s identity we know that:
x
x
We raise both sides of equation (1) to the 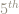 power:
power:
x
x
The left hand side of equation (2) is  .
.
x
The right hand side of equation (2) is, by the binomial theorem:
x
x
We separate the expression in (3) into real and imaginary parts, and equate the real part to -1, and the imaginary part to 0:
x
x
x
We can substitute 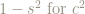 in (5) to get:
in (5) to get:
x
x
Expanding (6) and dividing through by  we get:
we get:
x
x
This is a quadratic equation for  with roots
with roots 
x
This gives 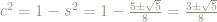
x
Only one of these two roots can be equal to 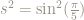 .
.
x
Which one?
x
We know  so
so  .
.
x
Therefore, 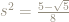 so
so  which means, since
which means, since  , that:
, that:
x
x
One can also get the quadratic equation for  from the multiple angle formulas (if one can remember them!).
from the multiple angle formulas (if one can remember them!).
Shoot me now! (Math jokes)
Posted by: Gary Ernest Davis on: December 2, 2010
