The number 3608528850368400786036725
Posted by: Gary Ernest Davis on: February 21, 2015
Ben Vitale (@BenVitale) announced that 3608528850368400786036725 is  a 25 digit number with the property that  each number formed by its first n digits is divisible by n, for n from 1 through 25.
How could we find similar numbers, and could there be a larger number than 3608528850368400786036725 with this property? (which we will call the Vitale property)
The numbers with 2 digits having the Vitale property are just the even numbers between 10 and 98.
We will investigate this issue using Mathematica®, so here’s our list of such 2 digit numbers generated in Mathematica®:
vitaleproperty[2] = Range[10, 99, 2]
{10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50,
52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,98}
How about numbers with 3 digits with the Vitale property?
They have to be obtained from even numbers by adding a digit to the left, and must be divisible by 3.
Here’s how Mathematica® can generate all the numbers obtained by appending a digit from a given number:
adddigits[n_] := Table[FromDigits[Append[IntegerDigits[n], d]], {d, 0, 9}]
For example, here’s what we get by applying the adddigits function to 248:
adddigits[248]
{2480, 2481, 2482, 2483, 2484, 2485, 2486, 2487, 2488, 2489}
To obtain 3 digit numbers with the Vitale property we have to append a digit to even numbers, and check which resulting 3 digit numbers are divisible by 3:
Cases[Flatten[Map[adddigits, vitaleproperty[2]]], x_ /; Mod[x, 3] == 0]
 {102,105,108,120,123,126,129,141,144,147,162,165,168,180,183,186,189,201,
204,207,222,225,228,240,243,246,249,261,264,267,282,285,288,300,303,
306,309,321,324,327,342,345,348,360,363,366,369,381,384,387,402,405,
408,420,423,426,429,441,444,447,462,465,468,480,483,486,489,501,504,
507,522,525,528,540,543,546,549,561,564,567,582,585,588,600,603,606,
609,621,624,627,642,645,648,660,663,666,669,681,684,687,702,705,708,
720,723,726,729,741,744,747,762,765,768,780,783,786,789,801,804,807,
822,825,828,840,843,846,849,861,864,867,882,885,888,900,903,906,909,
921,924,927,942,945,948,960,963,966,969,981,984,987}
 These are the 3 digit numbers divisible by 3, who’s first 2 digits are divisible by 2.
This suggests how we can recursively build n digit numbers with the Vitale property, from n-1 digit numbers with the Vitale property:
vitaleproperty[n_] := vitaleproperty[n] = Cases[Flatten[Map[adddigits, vitaleproperty[n – 1]]], x_ /; Mod[x, n] == 0]
For example:
vitaleproperty[4]
yields:
{1020,1024,1028,1052,1056,1080,1084,1088,1200,1204,1208,1232,1236,1260,1264,
1268,1292,1296,1412,1416,1440,1444,1448,1472,1476,1620,1624,1628,1652,1656,
1680,1684,1688,1800,1804,1808,1832,1836,1860,1864,1868,1892,1896,2012,2016,
2040,2044,2048,2072,2076,2220,2224,2228,2252,2256,2280,2284,2288,2400,
2404,2408,2432,2436,2460,2464,2468,2492,2496,2612,2616,2640,2644,2648,2672,
2676,2820,2824,2828,2852,2856,2880,2884,2888,3000,3004,3008,3032,3036,
3060,3064,3068,3092,3096,3212,3216,3240,3244,3248,3272,3276,3420,3424,3428,
3452,3456,3480,3484,3488,3600,3604,3608,3632,3636,3660,3664,3668,3692,3696,
3812,3816,3840,3844,3848,3872,3876,4020,4024,4028,4052,4056,4080,4084,
4088,4200,4204,4208,4232,4236,4260,4264,4268,4292,4296,4412,4416,4440,
4444,4448,4472,4476,4620,4624,4628,4652,4656,4680,4684,4688,4800,4804,
4808,4832,4836,4860,4864,4868,4892,4896,5012,5016,5040,5044,5048,5072,
5076,5220,5224,5228,5252,5256,5280,5284,5288,5400,5404,5408,5432,5436,
5460,5464,5468,5492,5496,5612,5616,5640,5644,5648,5672,5676,5820,5824,5828,
5852,5856,5880,5884,5888,6000,6004,6008,6032,6036,6060,6064,6068,6092,
6096,6212,6216,6240,6244,6248,6272,6276,6420,6424,6428,6452,6456,6480,6484,
6488,6600,6604,6608,6632,6636,6660,6664,6668,6692,6696,6812,6816,6840,
6844,6848,6872,6876,7020,7024,7028,7052,7056,7080,7084,7088,7200,7204,
7208,7232,7236,7260,7264,7268,7292,7296,7412,7416,7440,7444,7448,7472,7476,
7620,7624,7628,7652,7656,7680,7684,7688,7800,7804,7808,7832,7836,7860,
7864,7868,7892,7896,8012,8016,8040,8044,8048,8072,8076,8220,8224,8228,
8252,8256,8280,8284,8288,8400,8404,8408,8432,8436,8460,8464,8468,8492,
8496,8612,8616,8640,8644,8648,8672,8676,8820,8824,8828,8852,8856,8880,
8884,8888,9000,9004,9008,9032,9036,9060,9064,9068,9092,9096,9212,9216,
9240,9244,9248,9272,9276,9420,9424,9428,9452,9456,9480,9484,9488,9600,
9604,9608,9632,9636,9660,9664,9668,9692,9696,9812,9816,9840,9844,9848,9872,9876}
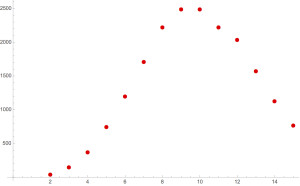
The size of the collection of n-digit numbers with the Vitale property grows with n for a while, but then begins to decrease:
T = Table[{n, Length[vitaleproperty[n]]}, {n, 2, 15}]
{{2,45},{3,150},{4,375},{5,750},{6,1200},{7,1713},{8,2227},{9,2492},{10,2492},{11,2225},{12,2041},{13,1575},{14,1132},{15,770}}
A plot shows this initials increase and then decrease quite markedly:
ListPlot[T, PlotStyle -> Red, PlotMarkers -> {Automatic, Medium}]
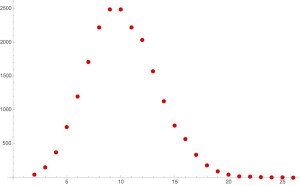
So, lets’s calculate, and plot, the number of n-digit numbers with the Vitale property versus n for n from 2 through 26:
T = Table[{n, Length[vitaleproperty[n]]}, {n, 2, 26}]
{{2,45},{3,150},{4,375},{5,750},{6,1200},{7,1713},{8,2227},{9,2492},{10,2492},{11,2225},{12,2041},{13,1575},{14,1132},{15,770},{16,571},{17,335},{18,180},{19,90},{20,44},{21,18},{22,12},{23,6},{24,3},{25,1},{26,0}}
ListPlot[T, PlotStyle -> Red, PlotMarkers -> {Automatic, Medium}]
So we see that there is exactly one 25 digit number with the Vitale property – the venerable 3608528850368400786036725 – and that appending any of the digits 0 through 9 to this number does not result in a 26 digit number that is divisible by 26. This means that 3608528850368400786036725 is the LARGEST number with the Vitale property.
Kudos to Ben Vitale for finding it!
Postscript: Éric Angelini points out that the number 3608528850368400786036725, and its properties discussed above, appears in the Online Encyclopedia of Integer Sequences.
Coffee, Love and Matrix Algebra – a review
Posted by: Gary Ernest Davis on: November 15, 2014
____________________________________________________________
Coffee, Love, and Matrix Algebra is a delightful work of fiction that chronicles the events of roughly a year in the life of the mathematics department at a university in Rhode Island. Can there be entertainment value in a book whose principal characters are math professors? Believe it or not, this is a page turner: The reader becomes emotionally invested in the ten to fifteen central characters and humor abounds throughout.
Many of the familiar features of academia are present. Faculty spar with administrators and faculty spar with faculty. In this particular department, there are essentially two groups: an energetic society of junior faculty engaged in exciting research, mostly in applied mathematics and/or statistics, and a smaller collection of senior faculty who no longer are — or never were — doing research. Members of the latter group for the most part stand in the way of the various initiatives that the younger faculty propose and strive to realize. Which group will exert more influence?
The main character is the very self-absorbed Jeffrey Albacete, whose fame in mathematics circles is due entirely to his very popular textbook Matrix Algebra, now in its 9th edition. Jeffrey is content, knowing that he is regarded internationally as an expert in matrix algebra. In Jeffrey’s opinion, the International Linear Algebra Society puts too much emphasis on linear algebra. The breakaway International Matrix Algebra Society, of which Jeffrey is a founding member and past president, puts the emphasis in the right place — on matrix algebra — and holds his textbookMatrix Algebra in high esteem. This is academic math humor done right.
Jeffrey enjoys sitting in his office and looking over all of the editions of his influential textbook. He also enjoys drinking coffee. Part of his routine is to walk to the campus gym, spend a few very leisurely minutes on the exercise bike, and then head over to the Daily Grind, a campus coffee shop. While he waits in line to order coffee, he counts the number of customers ahead of him in the queue and estimates the number of bricks on the wall. He muses about how humans start with counting and then progress to advanced topics like matrix algebra, of which he is an acknowledged expert. (Readers who share Jeffrey’s counting compulsion might want to count how many blueberry muffins he consumes over the course of the story.)
Fortunately, most of the abundant humor in the book derives neither from mathematical compulsions nor from the perceived strangeness of mathematicians. Most of the characters would be at home in any intellectual line of work, and much of the book’s humor in founded in the characters’ humanity, especially in their relationships with each other. Numerous ironic comments and observations, ranging from explicit to subtle, focus on characters’ foibles and interactions; the best of these remarks are worthy of Austen or Trollope. So one need not be a math professor to enjoy the book, although it is undoubtedly helpful. Granted, plenty of the mirth derives from the absurdities of academia, and the story delights those of us on “the inside†because it paints such an accurate picture of our work lives. Thankfully, however, perhaps even this academic humor can find an audience beyond the ivory tower: When situations arise that might be opaque to “outsiders,†the author routinely devotes a paragraph to spelling things out.
The characters who receive the most favorable treatment in the book — including those outside the university — are young, bright, driven, and for the most part technologically proficient. Their home is scientific computation, broadly defined, as they work to both advance and disseminate knowledge. One character who does not dwell in this realm is Alex the dog, who like Snoopy doesn’t talk but has powers beyond those of the typical canine. Another non-human character is perhaps the author’s favorite: Wolfram Research’s Computable Document Format. It is lauded throughout, even to the point that on more than one occasion someone conjectures that MathWorks must be sweating bullets.
Most of the main characters have good intentions as they strive to excel at their jobs and positively influence those around them. The characters frequently offer each other (and us) a healthy dose of simple wisdom, such as to view the vagaries of life not as problems but as opportunities. Over the course of the story, the optimistic and energetic characters do exert an influence on the pessimistic and moribund, but exactly how I will leave to the reader to discover. This is an enjoyable read and highly recommended.