Computational media: the universal acid of mathematics teaching (3)
Posted by: Gary Ernest Davis on: December 23, 2009
Calculators and computers as shortcuts
I recently sent out the following tweet:
republicofmath Should we continue to focus on basics of pencil and paper calculation, especially in early years? http://bit.ly/5iqPYL #math #technology
and got the following replies:
- stephenwuebker @republicofmath yes! One needs to know how and why calculations work before taking shortcuts w/ computers and calculators
- mathheadinc RT @republicofmath @stephenwuebker yes! One needs to know how & why calculations work before taking shortcuts w/ computers & calculators.
about 3 hours ago · reply · dm rt · - meepbobeep Tru RT @republicofmath @stephenwuebker yes! 1 needs to know how & why calculations work before taking shortcuts w/ computers & calculators.
So I want to address the issue of whether computers and calculators – in other words, forms of computational media – are “shortcuts”, and whether, as is implicit in the responses, using them first takes away the possibility , or probability, of knowing how and why a calculation works.
Knowing how and knowing that
Knowing how to do something is pretty important in many aspects of life. It’s also fairly easily tested or checked by asking a person to carry out the procedure that demonstrates they know how.
 For example: do you know how to ride a bicycle?
For example: do you know how to ride a bicycle?
Unless you are Lance Armstrong you will find it very difficult to demonstrate by talking about it that you know how to ride a bicycle.
To show that you can you simply get on a bicycle and ride it. Can you ride it with no hands? Well, show us and we will be convinced.
Demonstrating mathematical know-how usually requires a student to  perform under a variety of contexts before a teacher is convinced they truly know how. For instance, we can ask a student if they know how to solve quadratic equations. If they answer “yes”, they choose an equation to solve, and they solve it by factoring, or using the quadratic formula then we are perhaps moderately convinced that they know how. The point is that there are several different possibilities for the solutions of a quadratic equation, and we would like to see a student demonstrate proficiency in all these cases. So, typically, we test and grade them on their know how in solving quadratic equations.
Know-how is knowledge demonstrated in action – procedural memory. It relies on memory that is stored mainly in the parts of the brain that handle motor memory. Â It is generally quite difficult for a student to elaborate on their know-how by talking about it, just as it is hard to describe how to ride a bicycle, and much easier to demonstrate it, if you are able.
There seems to be a very good reason this is so. The parts of the brain that store and retrieve motor memories do not readily give or receive data from the parts of the brain that deal with our ability to declare, and articulate what we know. This is a different form of memory, handled by a different memory system from motor memory, and is generally known as declarative memory. Among other things it handles “knowing that”.
A big problem for mathematics teachers is to know how (pardon the pun!) to take the know-how of students, get it out on the table for them to examine, and form declarative memories that students can later use in different settings. For example, although students might demonstrate solid and stable know-how for solving quadratic equations (a less common occurrence than we would hope for), it is a common observation than when such students encounter quadratic equations in other settings – elastic collisions, or eigenvalues of matrices, for example (you can think of more example) – their apparently stable knowledge of quadratic equations now appears very unstable.
This is the phenomenon of inflexibility of knowledge: an inability to transfer knowing-how in one context to knowing-how in a different but related context. For a student’s knowledge to be flexible in this sense it seems they have to transfer knowing-how – in motor memory – to knowing-that – in declarative memory. How does a teacher help them do that? To the best of my knowledge no-one on this planet has an answer to that question.
Ability to carry out calculations, for young children and less experienced students, Â is knowing how. The memory of that knowing how resides largely in the motor cortex – memory of what the hands and fingers do in moving a pencil to carry out the calculation. Try this: for a student, or child you know, who is just learning to subtract two, or three digit numbers, and is having some success, ask them to explain, without doing a sum, how they do it. Generally, they cannot. The memory of doing is not yet available to the declarative memory system.
There are some scandalous misrepresentations of knowing how in school and university mathematics. For example many people mistakenly believe that they know how to add, subtract, divide and multiply decimal numbers when they do not. It is possible to do these things with some sophisticated knowledge, but most people do not have that knowledge. To see the problem, try to add as decimals; in other words, just by operating on the infinite decimal strings, and not by doing fraction addition and converting to a decimal. Â The problem of course, is that the carrying you have to do keeps getting pushed further to to the right. We need to know how to do an infinite carries. This is a consequence of the base 10 representation, with only the ten numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The same is true, of course, in any other base. Â So most people do not have the know how to do this, but simply assert that “it can be done.” [A student would not be allowed to get away with that on a test.]
Knowing why
“Understanding’ is a very tricky word in education and psychology, and I would rather avoid it.  However, knowing how has very little to with what I think of as understanding.  To get to understanding we seem to need to have insights into  how something works, and not just be able to demonstrate that we can do it. For example, if a student could solve quadratic equations by completing the square, and explain at each step why the calculations were valid, I would be more inclined to say that student “understood” solution of quadratic equations. Such a student has insight into the reason the calculation works.
Knowing why is , in my view, a whole different memory system than knowing how and knowing that. It is, essentially, memory for explanations.
Here is a simple example of knowing why. Let’s build a line of 1″Â 1″ squares, each square hard up against the previous one in the line:
 How does the perimeter of the line of squares change with the number of squares?
How does the perimeter of the line of squares change with the number of squares?
Typically, in elementary school, teachers get students to make a table and spot and describe a pattern:
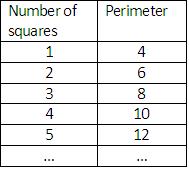 One way to describe this pattern is: the perimeter goes up by 2 each time we add a square.
One way to describe this pattern is: the perimeter goes up by 2 each time we add a square.
This is knowledge that – semantic knowledge, knowledge of a fact
Knowing why – knowledge of explanation – Â requires insight into the process of building the line of squares:
When a new square is added to an existing line  the 4 edges of the new square would add 4 to the perimeter, except that the two red edges shown will no longer be part of the perimeter. So the perimeter increases 4-2=2 each time a new square is added.
This insight is knowing why. Memory of this insight is memory for explanations. Knowing why is different from knowing how and knowing that.
What sort of memories do our students form?
There are many things even in elementary mathematics that we know how to do, we know that we can do them, but we, as adults and teachers, may not know why the procedure works. Two such examples are long division and standard algorithms for addition, subtraction and multiplication of whole numbers. As adults with lots of experience, both doing and explaining how to do, we have solid knowledge how to do these things, and to articulate how to do them. Much less commonly do we have any idea why they work – we may have little to no insight into why these procedures always give a correct answer.
Knowing why any algorithm works is not common, in my experience, in school mathematics. Teaching is first about having students know how to carry out the algorithm and then, if we are lucky, about being able to articulate that the algorithm works and use it in novel contexts. Expecting insight into why an algorithm works is not commonly part of school mathematics, either for students or for teachers.
So, in school mathematics we are  most often forming motor memories, of knowing how to do something, and declarative memories, of knowing, and articulating, that we can do it. Less commonly do we expect knowledge why – insight into a procedure that explains why it works, as in the line of squares example above.
Algorithms and knowledge
Here’s an interesting bit of history: the word “algorithm”  comes from “algorism” which, in turn, is an Anglicization of the name of the 8th century Persian mathematician AbÅ« Ê¿AbdallÄh Muḥammad ibn MÅ«sÄ al-KhwÄrizmÄ« who lived and worked in Baghdad.
An “algorithm“, which is what we commonly teach even in the earliest years in school , is a mechanical method for carrying out a procedure. Â Al-Khwarizimi wrote about mechanical means of adding, subtracting, multiplying and dividing fractions.
Being mechanical procedures, the standard algorithms of arithmetic can be, and have been, implemented on machines, and those machines are commonly known as calculators. Â Calculators are machine implementations of arithmetical algorithms (and much more).
So what are we shortcutting by getting students to use machines that implement algorithms? One thing we are shortcutting is having student behave like machines. Â Some people, and I am one of them, think this is a good thing.
Now I am guessing that my thoughtful, intelligent twitterers, meant something different by shortcutting. I am guessing they meant something like “failing to develop a number sense”. I am in complete agreement with a need for all students to have a strong number sense, by which I mean two things: a strong awareness of the number operations and their properties, particularly the distributive property, and an ability to estimate.
The machine implementation of algorithms – the calculator – Â impels us to ask the question: what is about practicing algorithms – the know-how of doing sums – that develops number sense, and what is it about using calculators that inhibits, or shortcuts, development of number sense?
I think this is a question worth asking, and it is computational media that pushes us to ask it.
Computational media: the universal acid of mathematics teaching (2)
Posted by: Gary Ernest Davis on: December 21, 2009
Coping in a time of rapid change
 At the end of this post I will tell you why I have stopped wearing my watch. It’s a lovely watch, given to me a year ago, on my birthday, by my wife. But I have recently stopped wearing it.
At the end of this post I will tell you why I have stopped wearing my watch. It’s a lovely watch, given to me a year ago, on my birthday, by my wife. But I have recently stopped wearing it.
Several people have contributed comments to  “Computational media: the universal acid of mathematics teaching (1)“. Thank you. Many people tweeted comments – thanks to you all.
A theme running through several comments is that  we should continue to focus on basics of pencil and paper calculation, especially in the early years.  Not uncommonly many people also were opposed to “mindless” pushing of technology buttons.
It’s hard to imagine (am I simply lacking imagination?) that any educator would actually support mindless pushing of technology buttons!  So I wanted to say that  this mindless pushing of buttons issue was a bit of a straw man, except that there is something there to worry about. We DO see kids mindlessly pushing calculator buttons to get a result that they want to proudly present as “the answer”. We do see, if we look hard enough, legions of users of statistical packages simply pushing buttons to carry out a test, for which they cannot properly interpret the result.
Just this week one of my calculus 3 students, unable to calculate a triple integral in spherical coordinates entered the integral into his TI 89, pressed a button, and got “the answer” ! Unsurprisingly, the calculator got the correct answer. Of course if the student had made a slight error in entering the integral, or had pushed the wrong button, he would have likely got a different, wrong “answer”, and would be none the wiser.
But is this all the fault of mindless button pushing. Couldn’t the way we teachers phrase the questions have a lot to do with it? My calculus 3 student was asked to use spherical coordinates. He forgot how. Being an engineering student who wanted a result, he did the next best thing – he used his TI 89 calculator. His method has more to do with a way of being an engineer, than with having knowledge appropriate to an engineer. Professional engineers, in other words, if they ever had to actually calculate a triple integral, would most likely use their calculators or other computational media. This student did what a sensible professional would do. Did he “understand” why the integral came out the way it did. No, but does anyone, even those who calculate on paper?
Hidden agendas
If we teachers ask a student to calculate something, we rarely are interested in the answer, the product. Because we have another goal in our teaching – to understand the utility of spherical coordinates, or to systematically solve linear equations – we are interested in the process of solution – the student’s working.
Many years ago I heard an apocryphal story that went along these lines: on a final philosophy examination at Cambridge, there appeared the question: “Can you explain Wittgenstein’s picture theory of propositions?” A student having no idea answered honestly: No”. The philosophers, realizing the irony of the situation, had to award the student full marks for the answer.
When we ask students to calculate something we usually have a hidden agenda. A well-attuned student knows this and is careful to give us what we want. But even if we ask a student to show their working, they could draw a picture of themselves pressing the calculator button. That is a truthful and full answer to our question, yet it usually will not satisfy is. Why not? Because we have an agenda which we have not fully disclosed to the students.
It seems to me that when we want to prohibit students using calculators because (a) they enjoy it (it’s pretty powerful!) and (b) it gives an answer, we are objecting because we have another agenda. This agenda is part of our educational aim, our background mental model of what education is about. But how can a child or student know that? They cannot, and the best they can do is to look carefully at our facial expressions, responses, or comments on their test papers, and try to guess what what will satisfy us. With the best intentions in the world, we train students to guess our intentions and give us what we want. When they do that we call them good students, good learners, and we think of ourselves as good teachers.
Bringing hidden agendas into the light
So, with that in mind, here is what I am saying about the rapid increase in powerful computational media available to students: computational media is forcing us to re-think what educational agenda we have in teaching mathematics, and why we have that agenda. It is stimulating debate, because it puts incredible power in the hands of students.
This is not a matter of  taste, or ideology, or opinion, whether you think  calculators or computers should or should not be used, in this grade or that. What it is about is the powerful wave of computational media that is compelling us to think about what we teach and why. Why is this inescapable? Because  it results from infrastructural changes in the way of being of young people. An old order is dying and a new one is coming in. We will have to adapt, not as partisans for or against calculators, or any other such computational devices, but as thinking human beings who are witnessing new ways of being.
To witness this change first hand, as it takes place in real time, engage with the debate on the use of cell phones in school. Many are against their use, some are for. My prediction is that within 2 years, it will be laughably old-fashioned not to use cell phones in your mathematics classroom, not to phone  a friend for an answer, but to do mathematics using currently available, cheap, powerful software.  Scary for a teacher who does not know how, exciting for those willing to take a chance.
Now my watch: I have not stopped wearing a watch because I am under 25 , but because I watched Ken Robinson talk about wearing watches [30.00 minutes into the video] and realized how laughably silly it now is.
The world is changing very fast. Our young students are used to technological change. We do not have to adopt the latest gizzmos or whizz-bang apps to do sensible empowering mathematics. But we will have to engage with what we teach and why. The kids’ use of technology will demand it.
Postscript
Imagine writing on paper and having that writing link automatically to deep computation. Futuristic?
Still not convinced the computational world is deeply changing our human experience? Take a look at Pranav Mistry’s TED talk.