Republic of Mathematics blog

This is a paper written for the Psychology of Mathematics Education conference in 2000. I am reproducing it here because I think it says something of value to mathematics teachers.

___________________________________________________________________________________

A memory-based model for aspects of mathematics teaching

Gary Davis, University of Southampton, Southampton, UK

David Hill, Hordle Walhampton School, Lymington, UK

Nigel Smith, Twyford School, Winchester, UK

Cite as: Davis, G., Hill, D., & Smith, N. (2000), A memory-based model for aspects of mathematics teaching. In T. Nakahara & M. Koyama (Eds.), Proceedings of the 24th Conference of the International Group for the Psychology of Mathematics Education, Vol 2, pp. 225-232. Hiroshima: Hiroshima University.

Abstract

We consider recent discoveries in brain function for declarative and procedural memories in the context of mathematical memory. These findings suggest to us a model for certain aspects of mathematics teaching, in which developing brains of children benefit from an external agent to assist in the formation of declarative memories from procedural memories. We consider implications of this model for classroom teaching.

Introduction

The nature of learning has been a constant area for research since the beginnings of modern psychology. Models for the activity of teaching, especially in the area of mathematics, have been much less common (see, however, Simon, 1995; Steffe and d’Ambrosio, 1995; and references). In this article we consider recent research into how human brains process declarative and procedural knowledge. On the basis of a simple but plausible assumption on the nature of developing brains we suggest that, at least in the early years of schooling, an external agent can greatly assist in the formation of declarative memories from procedural memories in mathematics. Given the importance of both procedural and declarative memories for mathematics, this suggests a significant function for a mathematics teacher: to fulfill that of an external conduit from one part of a student’s brain to another.

Declarative and procedural memory

Declarative memory (often referred to as explicit memory) is memory for facts and events, including scenes, faces and stories. Declarative memory depends upon having relevant brain structures intact: people with certain forms of amnesia, due to identifiable brain damage, lose their ability to function efficiently – or at all – with declarative memory (Squire, 1994, p.203). However, the concept of declarative memory is not due simply to disassociation of memory caused by brain damage: recent findings (for example, Eichenbaum, 1994; Ullman et al, 1997) demonstrate that specific areas of the brain are dedicated to declarative memory (see also, Bransford et al, 1999, p. 112 ff.)

Declarative memory includes episodic and semantic memory – a distinction due to Tulving (1983). This distinction is not sharp since in practice many memories involve both episodic and semantic aspects. The essential difference is that semantic memories are relatively bereft of context: they appear to the rememberer simply as known facts, whereas episodic memories involve significant components of context in which the memory was formed. The distinction in mathematical understanding is therefore critical because it relates to memories that have been pared down so as to be apparently free of context or irrelevant detail. In mathematics, episodic memories can facilitate the establishment of semantic memories (Davis, 1996).

Procedural memory is one form of non-declarative memory although the two are often identified as being the same. Cohen and Squire (1980) coined the term procedural memory for the ability to learn sensorimotor tasks in the presence of other severe memory losses. They postulated a memory for how to do things as distinct from a memory for what was done or what was recalled as a fact.

Declarative and procedural memory in mathematics

The distinction that is commonly made between declarative and non-declarative memory is particularly pertinent to learning mathematics. We take it to be the case that declarative memory – at least certain forms of it – in mathematics is a higher and more useful form of memory than procedural. This is because, in mathematics, we see declarative memory (memory that) as a form of extraction or compression of the essence of a procedure or procedures. Declarative memories in mathematics seem to associated with the formation of mathematical schema and the processes of encapsulation of procedures (ref. Tall et al, 2000). Indeed the original ancient Greek meaning was the “essence” of a thing: its characteristic nature.

A prime example of declarative memory can be observed in Maher and Speiser’s (1996) account of a young student who related binomial expansions to memories of building block towers. In using her memories of building block towers to establish a potent link between these towers and binomial expressions this student was able to declare that the binomial expressions were “just like” the towers. She effectively stopped carrying out the procedure of expanding the binomial expression and declared that it was just like building towers of height 3 from two colors of blocks.

Classic examples of procedural memories arise from students’ engagement with taught algorithms such as long division, multiplication of whole numbers, the Babylonian iterative method for finding square roots, the bisection algorithm for finding square roots, and Euclid’s algorithm for the greatest common divisor of two positive integers. It is a commonplace observation that many students learn to carry out these procedures but have great difficulty talking about them in the absence of doing them.

An almost universal example of a non-taught procedure that is recalled procedurally very well by children as young as 3 and 4 years of age is sharing, also known as dealing or distributive counting (Hunting and Davis, 1991; Miller, 1984). However these same children are largely unable to talk about and contemplate the act of sharing as a fact (Hunting and Davis, 1991).

Neurophysiology of declarative and procedural memory

A clue to the difficulty in articulating procedures in mathematics comes from work of Ullman et al (1997) on language difficulties in sufferers of Alzheimer’s disease on the one hand and Huntington’s and Parkinson’s on the other. Their work suggests that word memory relies on areas of the brain that handle declarative memory – memory of facts and events. These appear to be the temporal or parietal neo-cortex. However, rules of grammar seem to be processed by areas of the brain that manage procedural memory, the basal ganglia, which are also involved in motor actions. Declarative memory has been considered in detail by Eichenbaum (see, for example, Eichenbaum, 1994) who locates it primarily in the hippocampal system. This area of the brain is part of the limbic system, responsible largely for emotion and drives. The hippocampal system has many connections both to and from the temporal and parietal lobes of the neo-cortex. The current view suggests that for declarative memory, episodic memories reside largely in the hippocampal region whilst semantic memories reside principally in the neo-cortex.

A memory-based model for teaching mathematics

That there seem to be two distinct brain areas for procedural and declarative memory must make us suspicious. In mathematical settings, at least, the region devoted to declarative memory may have difficulty – that is, few mechanisms for – taking as its basic material the activities of the region responsible for procedural memory. If so, the role of teacher becomes even more evident: as an external conduit to allow declarative memories to be formed from the raw material of stored procedural memories.

A decisive force in the creation of mathematical schema may be an appropriate agent capable of externalizing procedural memory and utilizing it so that a student can form declarative memories, both episodic and semantic. The reason for this, we hypothesize, is that the temporal and parietal neo-cortex has, in young children, few mechanisms for taking the memory activities of the basal ganglia as raw data for the formation of new declarative memories. What has to happen, we suspect, is that an agent externalizes those memories of procedures from the basal ganglia and recasts them in a form suitable for the hippocampal region and/or the temporal and parietal neo-cortex to process them as declarative memories. Our model, building on what is known about brain structures for memory, has the following features:

1. There are, in young, developing brains, relatively few direct connections between the brain regions implicated in procedural memory and those implicated in declarative memory. There are known to be direct connections into the basal ganglia – responsible for motor control and planning – from all over the brain. We postulate that in younger brains there are few direct connections from the basal ganglia to the hippocampal region and/or the temporal and parietal lobes.
2. Episodic memory, as a form of declarative memory, resides largely in the hippocampal region.
3. Semantic memory, as a form of declarative memory, resides largely in the neo-cortex, particularly the temporal and parietal lobes.
4. An external agent can assist in the formation of episodic memory from procedural memory.
5. An external agent can stimulate pre-existing connections between the hippocampal region and the neo-cortex to assist in the transfer of episodic to semantic memory.

Focus of attention and the central role of episodic memory

In the enhancement of mathematical memory the major issue for a teacher to focus on is assisting students to establish appropriate episodic memories of mathematical activity. In our model of teacher as external agent, there are three possible ways in which the teacher can play a part in enhancing memory. These are, assisting in the transfer of:

1. procedural memories to episodic memories;
2. episodic memories to semantic memories;
3. procedural memories directly to semantic memories.

Not a lot seems to be known about the necessity of semantic memory building on episodic memory (Squire et al, 1993). We hypothesize that a direct transfer of procedural to semantic memory is unlikely to occur in the domain of mathematics. Such a transfer would involve establishing a mathematical fact or facts from memories that involve only habit or the execution of procedures, in the absence of episodic memories. An example might be a student who is involved in the practical successive approximation square roots of whole numbers declaring that the square root of a number is another number whose square is the first, without the intermediation of episodic memory pertinent to the approximation of square roots. This simply does not gel with our experience: students will speak about their experiences first by using episodic memory. It seems to us, therefore, that episodic memory plays a major role in the transition of procedural memories to semantic memories. In the formation of such episodic memories a student’s focus of attention is critical. This is because not everything about an episode is appropriate to recall for the purposes of obtaining a deeper understanding of the mathematics involved. The memory of it being a hot spring Friday afternoon in a class of 25 other students, all wearing jeans, is not relevant to the formation of episodic memories of factoring quadratic equations. What is relevant is a student’s memory of what they were doing, in a mathematical sense, as they factored a particular quadratic.

Implications of the model

Our brain-based model of teacher as external agent between an individual child’s procedural and declarative memories has implications for the sorts of activities that a teacher engages in to facilitate the formation of declarative memories. The most obvious implication is for what is likely not to work. Although we regard practice at procedures and algorithms as important, our model indicates that this alone will not be sufficient for all, or even a majority, of students. The ability to form declarative memories is not going to arise simply from carrying out procedures.

What might a teacher do to assist a student to form declarative memories from memories of procedures? One clue comes from the student studied by Maher and Speiser (1996). As a child in elementary school, building towers with her classmates, she persistently and habitually, asked why: “why is it so?” For example, upon finding 16 towers of height 4, she and the other children eventually argued that each tower of height 4 came from a tower of height 3, and there were exactly 2 ways to build a tower of height 4 from any given tower of height 3. This was their reason that the number of towers doubled as the height increased by 1. This, for them, was now a declarative fact. These children essentially acted as external agents for each other in turning procedural memories into declarative memories. The drive came from demanding an answer to “why?”. Asking why has to be an attractive proposition to a student: otherwise their answer to “why” may well be: “I don’t know. And I don’t care.”

Another clue comes from the central role of episodic memory- as a halfway house in the transition from procedural to semantic memory. One way to assist in the formation of episodic memories, focusing on aspects of episodes pertinent to understanding mathematics, is for a student to elaborate their solution procedures to problems through explanation and discussion. A student cannot talk about their solution procedures unless they have something episodic or semantic to talk about. This is because procedural memory, by its very nature as a form of non-declarative memory, is not accessible to verbal discussion (Squire, 1994). Insisting that a student talk about their solution procedures therefore forces them to bring to mind episodes in which they carried out those procedures. In other words, it forces them to establish declarative memory for procedures in the form of relevant episodes.

Finally, another implication of our model is that teachers need to ask themselves what is the nature of their own memories and types of understanding. This is because, as Ma (1999) points out:

“… none of those teachers whose knowledge was procedural described a conceptually directed teaching strategy. … Not a single teacher was observed who would promote learning beyond his or her own mathematical knowledge” (p. 54)

References

Bransford, J. D., Brown, A. L. & Cocking, R. R. (Eds.) (1999), How People Learn. Brain, Mind, Experience and School. Washington: National Academy Press.

Cohen, N.J. & Squire, L.R. (1980), Preserved learning and retention of pattern-analyzing skill in amnesia: Dissociation of knowing how and knowing that. Science 210, 207-210.

Davis, G. (1996), What is the difference between remembering someone posting a letter and remembering the square root of 2?. In L. Puig & A. Guttieréz, (Eds.) Proceedings of the 20th conference of the International Group for the Psychology of Mathematics Education, Vol 2, pp. 271-280. Valencia: Universidad de Valencia.

Hunting, R. P. & Davis, G. (1991), Early Fraction Learning. New York: Springer Verlag.

Ma, L.-P. (1999), Knowing and Teaching and Elementary Mathematics. New Jersey: Lawrence Erlbaum.

Maher, C. & R. Speiser, R. (1997), How Far Can You Go with Block Towers? In E. Pehkonen (Ed.), Proceedings of the 21st Conference of the International Group for the Psychology of Mathematics Education, Vol 4, pp. 174-181. Helsinki: University of Helsinki.

Miller, K. (1984), Child as the measurer of all things: Measurement procedures and the development of quantitative concepts. In C. Sophian (Ed.) Origins of Cognitive Skills, pp. 193-228. Hillsdale, N.J.: Erlabaum

Simon, M.A. (1995), Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26(2),114-145

Steffe, L.P. & d’Ambrosio, B.S. (1995), Toward a working model of constructivist teaching – a reaction to Simon. Journal for Research in Mathematics Education, , 26 (2), 146-159.

Squire, L. R. (1994) Declarative and non-declarative memory: Multiple brain systems supporting learning and memory. In D. L. Schacter & E. Tulving (Eds.) Memory Systems, 1994, pp. 203 – 231. Cambridge, Mass.: MIT Press.

Squire, L. R., Knowlton, B. & Musen, G. (1993) The structure and organization of memory. Annual Review of Psychology, 44, 453- 495. Reprinted in D. Shanks, Human Memory. A Reader. 1997, pp. 152 – 197. London: Arnold.

Tall, D. O., Thomas, M., Davis, G., Gray, E. & Simpson, A. P. (2000), What is the object of the encapsulation of a process? Journal of Mathematical Behavior, 18(2), 223-241.

Tulving, E. (1983), Elements of Episodic Memory. Oxford: Oxford University Press.

Ullman, M.T., Corkin, S., Coppola, M., Hickok, G., Growdon, J. H., Koroschetz, W. J. & Pinker, S. (1997), A neural dissociation within language: Evidence that the mental dictionary is part of declarative memory, and that grammatical rules are processed by the procedural system. Journal of Cognitive Neuroscience, 9(2), 266-276.

Teaching mathematics with technology

Recently I taught a graduate level course “Technology for Mathematics Teachers” in which undergraduates, in-service, and pre-service teachers of mathematics participated. An issue that arose early, and which dominated our discussions, was the lack of easy access to technology in classrooms. Some typical comments were:

• “Presently technology is not used in my teaching environment. Obstacles such as time, money, and curriculum deter teachers. I am working in a classroom which has one computer with limited access to the Internet. The main purpose of the computer is grading and email. The email system was designed basically to save on paper. Integrating technology in the classroom can be done with curriculum related projects. If the administration can be convinced technology will increase student test scores they would be more receptive to change. Teacher training is the key. If a teacher is trained and comfortable with the technology they could demonstrate its benefits. Once this benefit is demonstrated the next step would be to study and test the result of technology based curriculum verses the standard classroom. …  The environment of the classroom can be changed but it would take time, training, and money the schools may not be willing to invest. Technology can be brought into schools if the educator is persistent, knowledgeable, and convincing.”

• “Some of the most difficult perspectives of implementing technology in my classroom, or in my school, are very obvious. First, there are no computers in my classroom other than the teacher computer. This computer is regulated by the IT department in which they do not allow software to be installed without their approval – and that doesn’t happen without much time and red tape. Even trial or free software is prohibited most of the time. There is a laptop cart (two, exactly) that is available on a first come first serve basis and this is usually always taken by the English or history teachers who have regular needs for the computers. And again, there is the issue of software being installed – there isn’t any! If I’d like for my students to use technology, it would have to be with using something available on the internet alone, and that is usually not something that I can find that allows an entire class to work productively on Algebra 1, 2 or Geometry concepts.”

• “If teachers know how to use hardware, that doesn’t necessarily mean the students do. Teachers would need to devote ample time in teaching the students how to use any software even before they use it to teach a lesson. This takes time. Some students may know way more than others and begin to feel bored through any tutorials of how to use a program and start getting off task. It may even be a case of students lacking the interest that keep them unmotivated.”

Yet students do have a powerful technological tool with them: their cell, or mobile, phone. And students do not need to be trained how to use this technology – they are already way ahead of the curve. Additionally, the use of mobile phones in teaching and learning mathematics is being studied and analyzed in a number of countries.

Mobile phones and mathematics

What’s available?

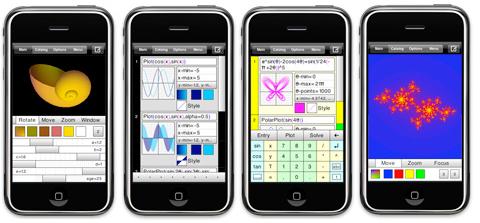
SpaceTime 4.0 is the killer app for iPhones and iPod Touch.

It also runs under Windows 2000/XP/Vista/7., Mac OS 10.4 and above, and Pocket PC (compatible with Windows Mobile 2003, 2003 SE, 5.x, 6.x)

Spacetime 4.0 is not free, but is available at a reasonable price for its outstanding capabilities: $99 for computer version, $79 for Pocket PC, $15 for iPhone or IPod Touch.

Math4Mobile develops Java  mobile phone apps for teaching and learning mathematics.

They have a Website a Twitter page, and a Facebook page.

This project is lead by Michal Yerushalmy of the Institute for Alternatives in Education at the University of Haifa.

x

iPhone apps. There are numerous iPhone apps that engage students in various aspects of  arithmetic, some are free, others range from $0.99 to a few dollars.

Sigma Centre for Excellence in Teaching and Learning (CETL) in the provision of mathematics and statistics support. This centre, run jointly by Loughborough and Coventry universities in the UK, produces videos on selected mathematical topics that are download-able to mobile phones. Currently their video tutorials are restricted to complex number topics.

Who’s doing what?

Nokia in South Africa. South Africa’s Department of Education is collaborating with Nokia and the nonprofit organization Mindset Network in a pilot project to improve the mathematical skills of tenth-grade girls. To do that, they have initiated a program called M4Girls, which uses Nokia cell phones that are loaded with mathematics.

Michal Yerushalmy, Professor of Mathematics Education, at the University of Haifa. She developed the Math4Mobile Java apps and works to implement these in classrooms in Israel.

Kevin Scritchfield, Fresno, CA, uses iPhones and/or IPod Touch in his classroom, according to Twitter reports.  I have yet to verify this with Kevin, but hope to very soon.

Ann Gregson, Concord, NC, has access to a set of iPod Touch which she uses to teach mathematics.

rachelala tweeted:

When a high school principal I lifted cell phone ban 5 years ago. It brought way more benefits than problems #edchat

Mingoville tweeted:

• lifting cell phone ban enabled students to use camera and calculator functions readily in lessons. and on trips
• Best e.g. was ‘challenging’ boy who re-did a Sci experiment at weekend, videod it and showed us on his phone on Monday

Xinyou Zhao & Toshio Okamoto, University of Electro-Communications, Japan, wrote an article on a Mobile Mathematics Tutoring (MoMT) system, which provides mathematics tutoring, exercises, and discussion for elementary students to improve their mathematical knowledge and skills:  Personalized_Mobile_Mathematics_Tutoring_System_for_Primary_Education

Mobile Devices in the Classroom. District Administration: the magazine of school district management. “Some districts and administrators are realizing the untapped potential of cell phones. It’s part of an “anytime, anywhere” learning movement that leaves laptops and even smaller netbooks behind, proponents say, in favor of more mobile, affordable and reliable handheld devices—from “smartphones,” which can run operating systems such as Windows Mobile and a host of software, to iPods, known more for playing audio and video but adaptable to more interactive applications through new educational platforms.”  Rest of article …

Geometry of the built environment

Several times when I have been engaging pre-service elementary teachers with geometry I have sent them out around campus with disposable cameras – usually one camera to every 2 students – to photograph geometric aspects of the built environment. Typically, they come back , talk about what they saw, with attempts at drawing, and I develop the film to give back next class and discuss again. My aim is to estimate where they are in the van Hiele level classification of geometric understanding, and to get them, as prospective teachers, to understand the van Hiele levels so they can tailor their own geometry lessons to their prospective student’s capabilities.

It is instructive to me, and to these prospective teachers, to see how some of them describe geometric figures in a very perceptual way as round, pointy, square, circles … and how others see more deeply into properties and relationships between properties.  Discussing their own level of understanding of geometry seems to  help them understand the geometry better and also help them think about how they would teach geometry.

Buying and distributing disposable cameras, collecting them, developing them, and handing out out prints, is a long and  time-consuming task. How much better to get students to take pictures with their cell phones, post the pictures to a blog or Flickr account, and share?

A junior high school teacher colleague is working with me to develop a unit on geometry of the built environment  for her year 10 students, most of whom avowedly hate geometry, remember little  to nothing of their grade school geometry, and keep asking her what use this is to their lives.

Opening their eyes to the geometry of the built environment that surrounds them – in school, at home, in the malls and shopping centers – may allow them to see the depth of thought that goes into the built environment in which we live, and to which someone contributed, and made a substantial living, as architect, designer, planner, builder, or client.  Her students will use their cell phones to take pictures of the built environment throughout the semester.

They will post to a blog, and discuss on the blog the features of their geometric postings. Currently she plans to spend a small amount of time each class having a couple of students discuss aspects of their blog postings.

________________________________________________________________

Thanks to the following tweeps for their input: @msgregson, @MikeCr, @Arithmeroo, @busynessgirl, @mrautomatic, @ottomaddock, @girlmeetsbike, @Algorithmist, @PR4Science

I would like to add to the brief samples of cell phone use in mathematics classrooms. Please share your experiences with me.